It's hard to open a web browser without being hit by gray, yellow, and green blocks. Perhaps you've been an avid follower for months. Or you might be like me: I tried it once, was completely confused, and shut it down. But I could not let a silly easy game beat me. Instead of enjoying it like a normal person, I put on my nerdy glasses and started typing in my jupyter notebook. This is my journey to beating Wordle: being able to determine every word in its dictionary with no exceptions (and no hacks).
About this project: I am doing this from my own time, but largely to advance my growing skills as a critical thinker and emerging coder. I want to gain better efficiency with Python and think like a programer. The code I share is full of un-optimal processes. Much of it is tyring to find a proof of concept. My goal was to optimize once I got a working model. I went through many iterations of a scoring method to suggest the best words. In the end, I only kept the structure of the class. My actual choosing and sorting method ended far differently than I spent most of my time on. So you can follow along with my thought process to eventually see how I got to the end. Or you can skip ahead to the end if you only really want to see the final form.
basic beginning imports:
import random
import statistics
import math
#Collins Scrabble Words 2019
with open('CSW2019.txt') as file:
all_words = file.read().lower().splitlines()
all_words = all_words[2:]
len(all_words) #279496
#list comprehension
[word for word in all_words if len(word) == 5]
I used this comprehension for a long time before improving dictionary source (later)
To do this I needed to make this a class.
class wordle_game:
def __init__(self, dictionary, word_length=5):
self.word_length = word_length
self.available_words = [word for word in dictionary if len(word) == self.word_length]
self.guess_words = self.available_words.copy() # because I know I want to reduce this while keeping the original intact
#now here is what we need for scoring:
self.all_letters = []
# this list will contain _every_ letter in every five letter word in the english dictionary.
#is this efficeint? no. But do I care? not yet. First things first
self.global_letters_count = 0
#number of all letters. I could sum() the all_letters, but for now I want to add as I go later
self.global_letters = dict()
#keys will be letters a-z
self.local_letters = [dict() for i in range(self.word_length)]
self.local_letters_count = [0 for i in range(self.word_length)]
#Make a dict for each slot (one for each five letters)
#These dicts will contain letters a-z for each slot
#Prepare to tally the sum of entries per slot
This isn't overly efficient. But will get us going to see if the theory will work. Now, lets set up some class methods. The purpose of each method is pretty self explanetory
#I'm going to call the analyze controller whenever I want to score or rescore after the available words change
def analyze(self):
self.count_letters()
self.letter_share()
self.score_words()
#make sure to initiate the process at __init__
def __init__(self, *):
...
...
self.analyze()
Below we are hard counting each letter. more efficeint ways exist. But this allows me to see what's going on sequencially.
def count_letters(self):
for word in self.guess_words: #this is the copy of dictionary above. It will modify as we eliminate words
for i,l in enumerate(word): #get each letter one at a time
self.all_letters.append(l) #this will add all letters to above list
if l not in self.global_letters.keys():
self.global_letters[l] = {'count':0,'share':0} #add each letter to global dict
self.global_letters[l]['count'] += 1
self.global_letters_count += 1
if l not in self.local_letters[i].keys(): #now we use i to determin slot in word
self.local_letters[i][l] = {'count':0,'share':0}
self.local_letters[i][l]['count'] += 1
self.local_letters_count[i] += 1
Create a percentile of frequency. This will be the basis for scoring
def letter_share(self):
for l in self.global_letters.keys():
self.global_letters[l]['share'] = self.global_letters[l]['count']/self.global_letters_count
#We are dividing the total number of occurences of each letter by all letters ever used
#I call this 'share'. It represents the percentage or share each letter gets globally
for i,letter_dict in enumerate(self.local_letters):
for l in letter_dict.keys():
letter_dict[l]['share'] = letter_dict[l]['count']/self.local_letters_count[i]
#I find the share of each letter in each slot by its slot count
Here is where the experimentation begins. I don't know what the relationship is yet between letters global and local usage. I need to find patterns and experiment with combinations.
def score_words(self):
self.words_by_score = dict() #I don't like making class attributes in a method. but I also want to reset it each time.
self.score_by_letter(self.words_by_score,self.guess_words) #this seems redundant. But I'm going to add to this later
def score_by_letter(self, scoring_dict, word_dict):
for word in word_dict:
local_score = 0
global_score = 0
for i,letter in enumerate(word):
local_score += self.local_letters[i][letter]['share']
#We are summing the frequency of letter usage in each local position
for letter in set(word):
global_score += self.global_letters[letter]['share']
#We are summing the frequency of each letter usage globally
sc_added = local_score + global_score
sc_prod = local_score * global_score
sc_sq_added = local_score**2 + global_score**2
sc_sq_prod = local_score**2 * global_score**2
sc_loc_to_glob = local_score / global_score
sc_glob_to_loc = global_score / local_score
scoring_dict[word]={
'local':local_score,
'global':global_score,
'sc_added':sc_added,
'sc_prod':sc_prod,
'sc_sq_added':sc_sq_added,
'sc_sq_prod':sc_sq_prod,
'sc_loc_to_glob':sc_loc_to_glob,
'sc_glob_to_loc':sc_glob_to_loc
}
So far, my chosen methods for scoring words are:
I'm going to have to enumerate through all my options and see which scoring method works the best.
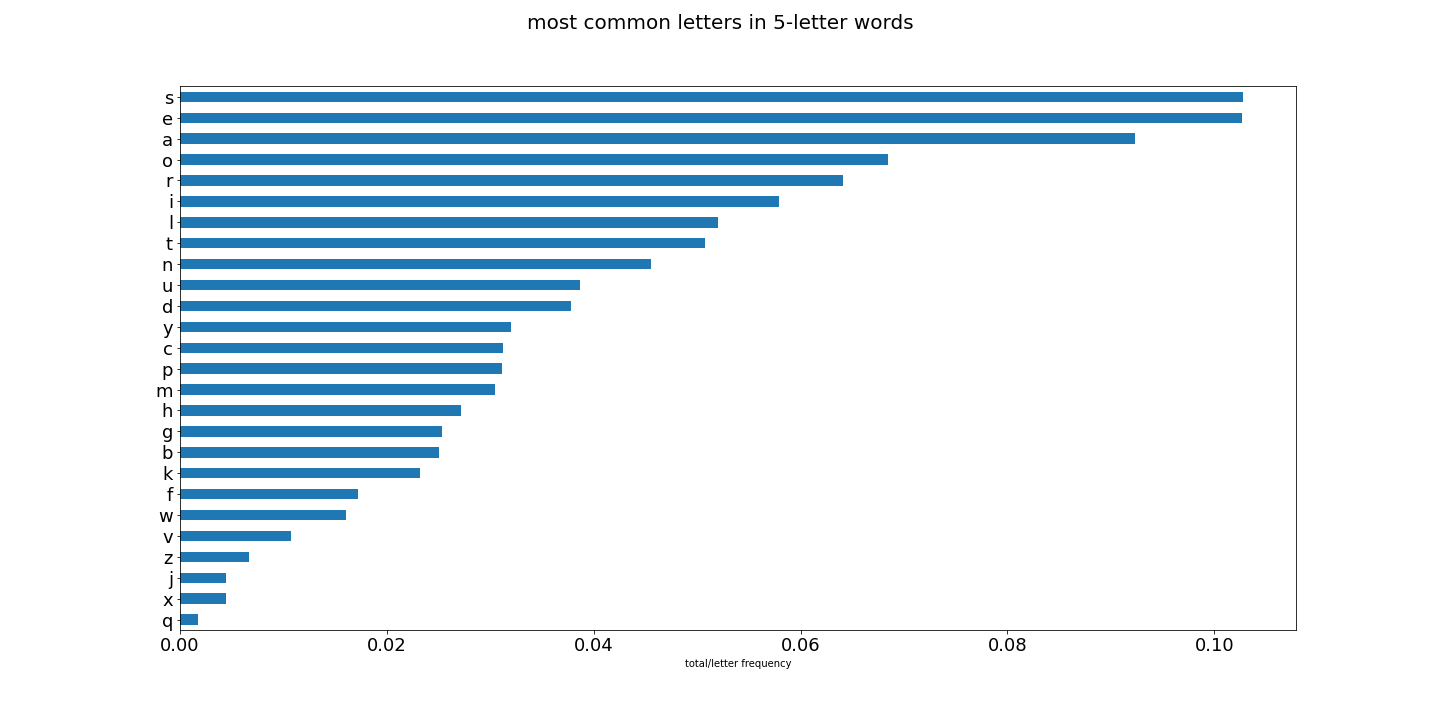
First, let me show you some graphs of results for letter usage:

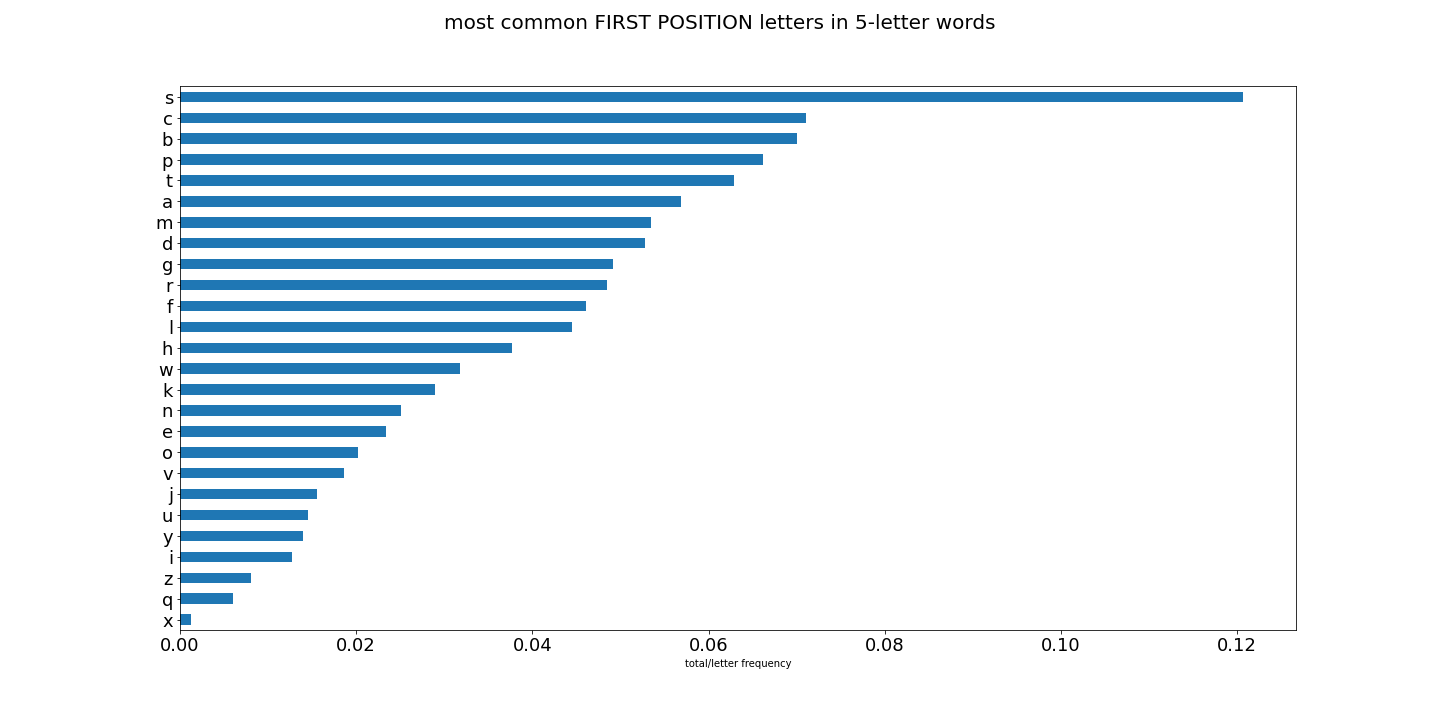
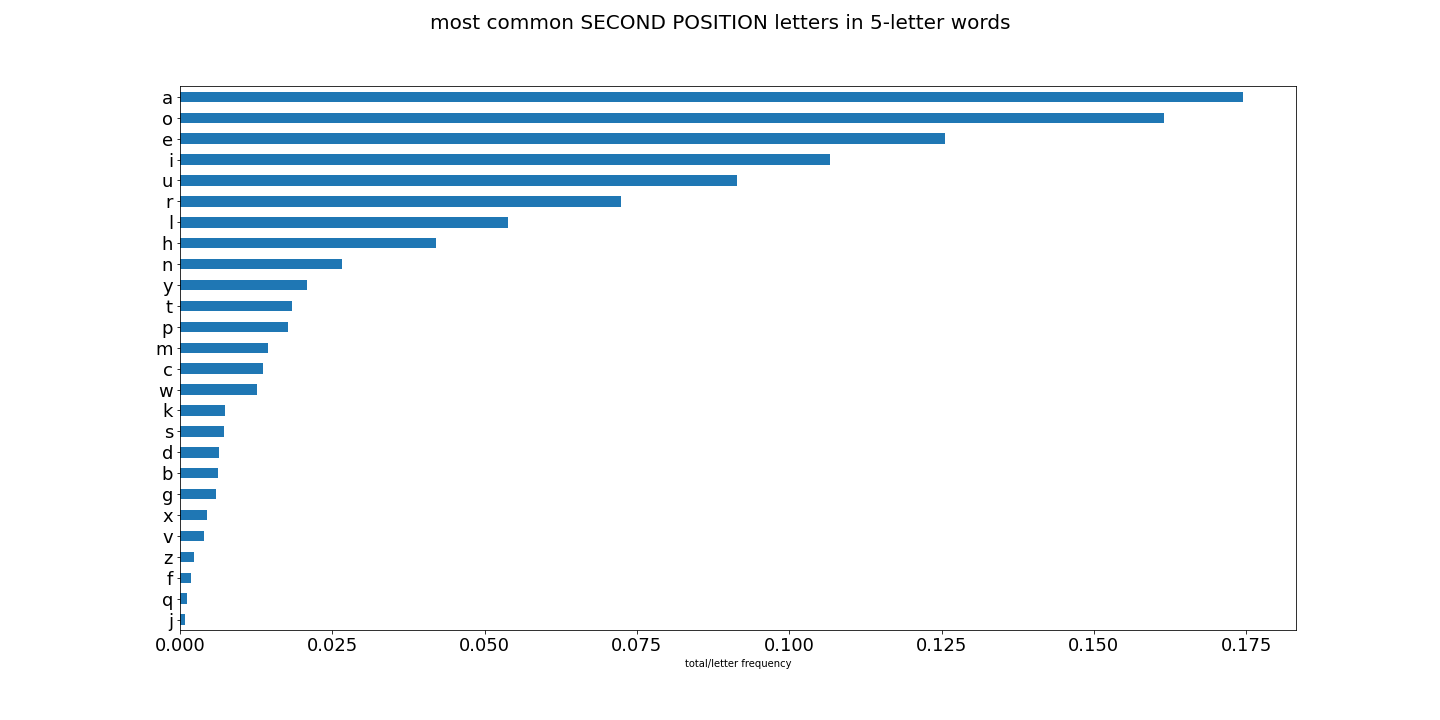
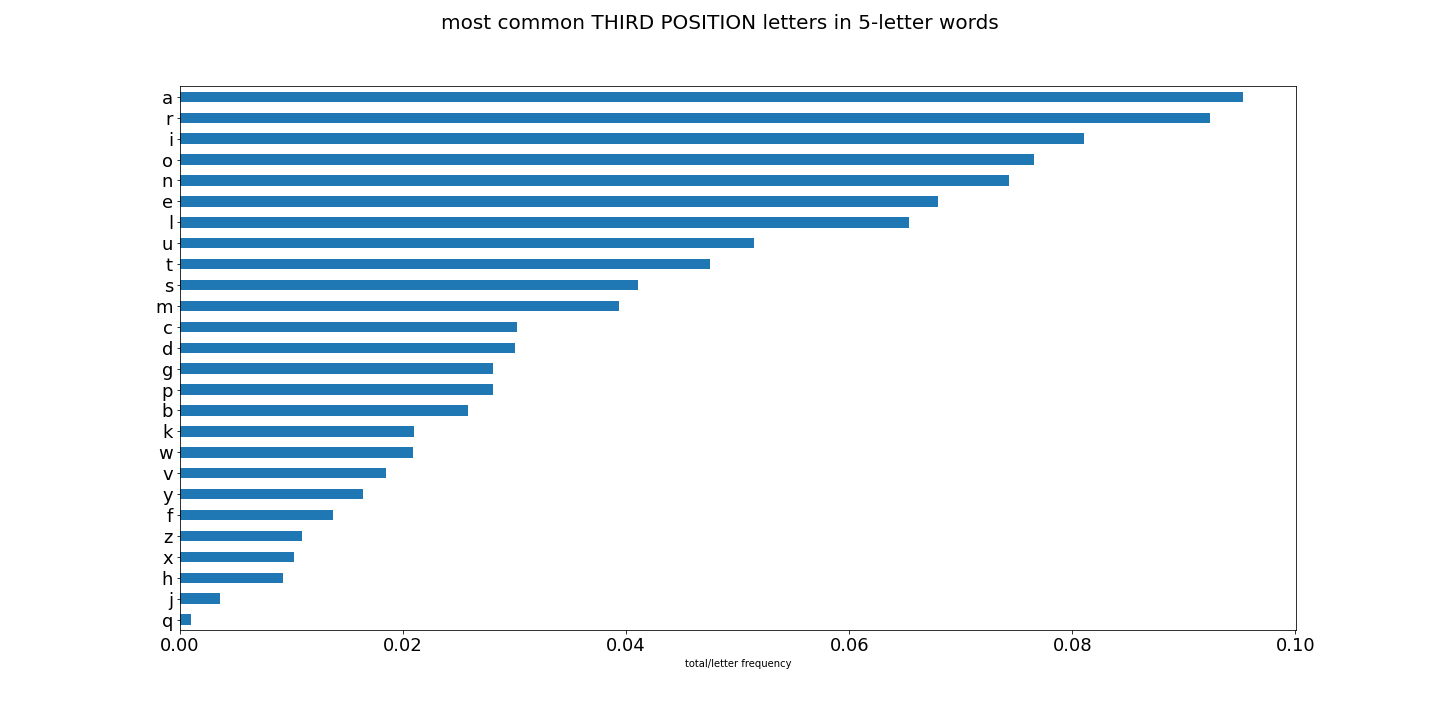
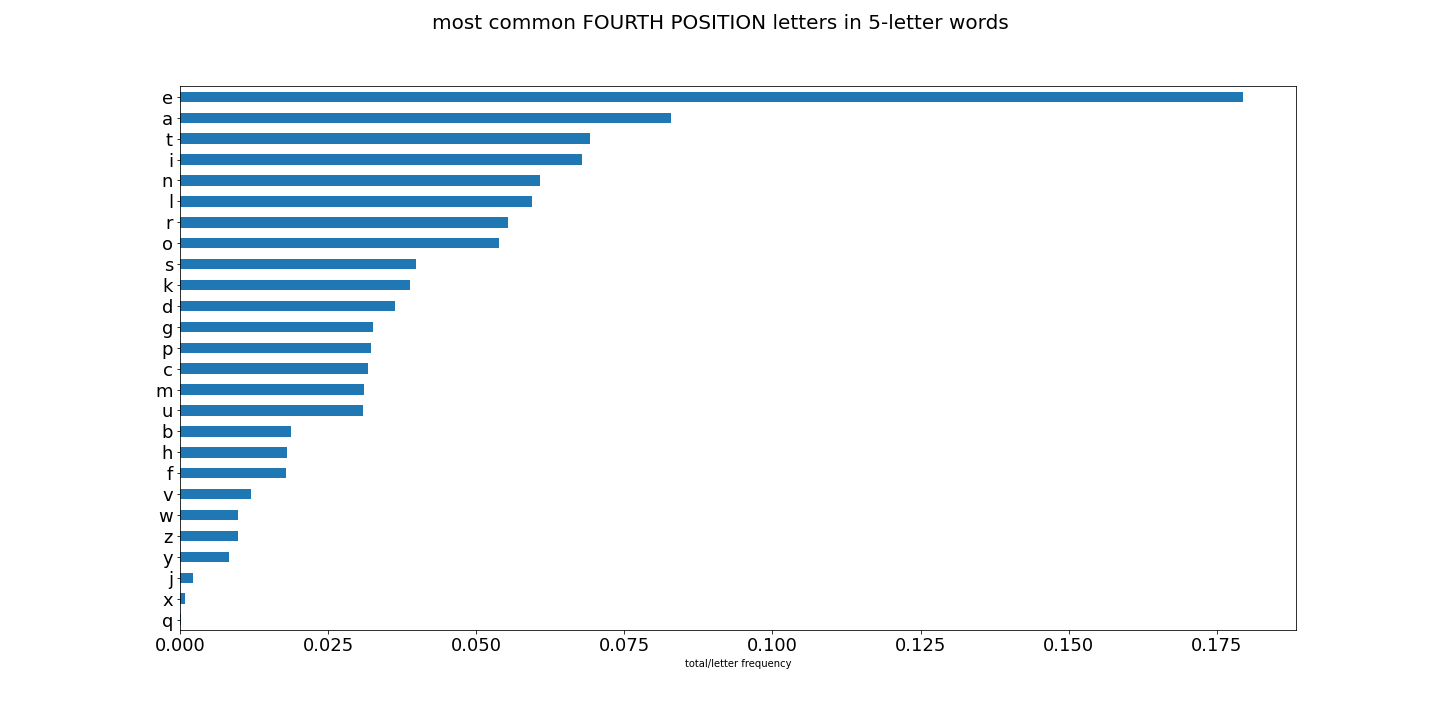
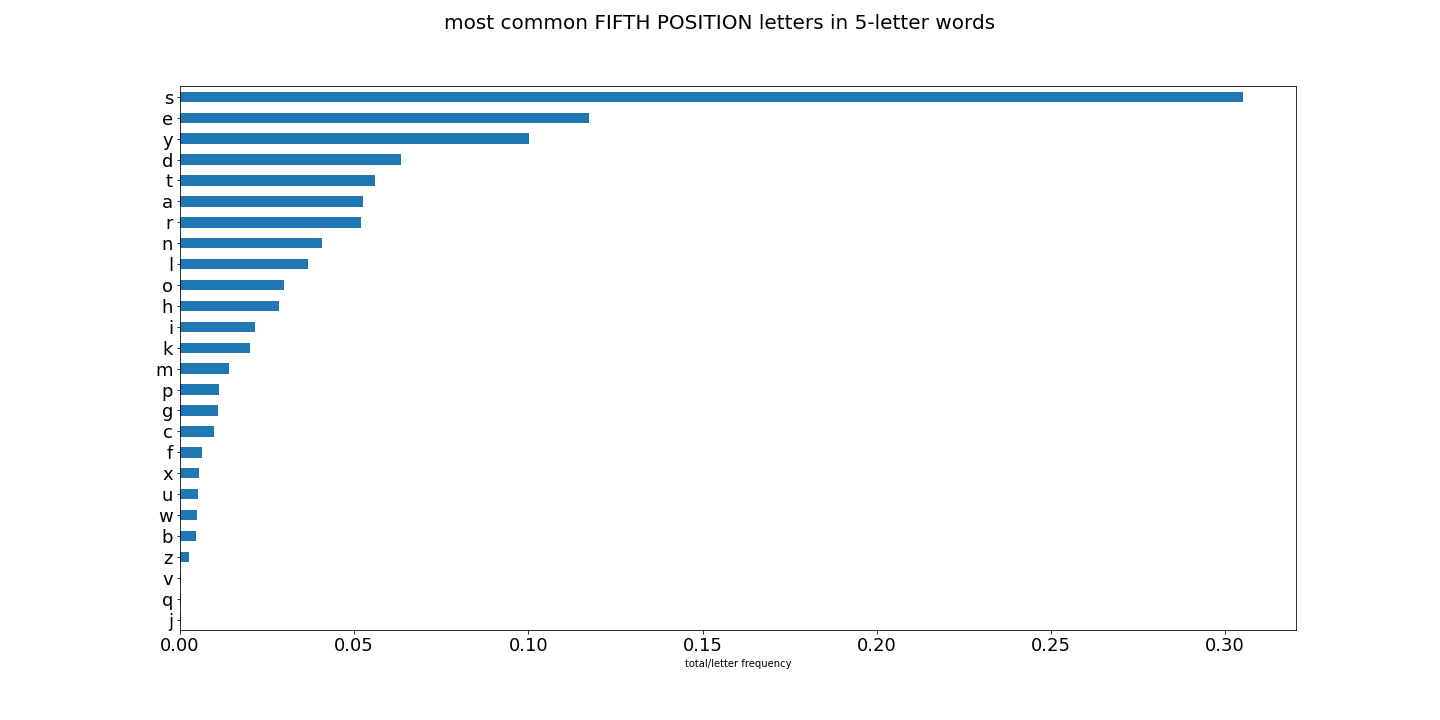
Lots of interesting things going on here. And great for constructing words to narrow down our Wordle guess. So now that we have all the letters in the english language score globally and locally, and then have all words scored by the eight methods above, we can start finding the top words scored by each method. These words should give us the best initial guess word.
Here's our official suggestor
def suggest(self,method="sc_prod"):
suggestions = self.top_words(self.words_by_score, method,10)
return suggestions
def top_words(self,word_dict,method,n=10):
sorted_words = sorted(word_dict, key=lambda x: (word_dict[x][method]),reverse=True)
top_n = sorted_words[:n]
return top_n
The top guesses for each of the eight methods is as follows:
| score_method | word |
|---|---|
| local | 'sores' |
| global | 'aeros' |
| sc_added | 'tares' |
| sc_prod | 'tares' |
| sc_sq_added | 'sores' |
| sc_sq_prod | 'tares' |
| sc_loc_to_glob | 'susus' |
| sc_glob_to_loc | 'ethyl' |
First, we need to add a few more attribues to our __init__ to track our guessed letters
Second, we need to set a game_word attribue for testing.
def __init__(self,*):
...
...
self.guess_count = 0
self.guesses = list()
self.correct_position = [0 for i in range(self.word_length)]
self.letters_in = set()
self.letters_out = set()
def set_word(self, word_to_use):
self.game_word = word_to_use
Now we can create a guessing method
def guess(self, word):
word = word.lower()
answer = []
#We are going to replicate the Wordle scoring.
# 0 == gray ; 1 == yellow ; 2 == green
for i,letter in enumerate(word):
if letter == self.game_word[i]:
answer.append(2)
elif letter in self.game_word:
answer.append(1)
else:
answer.append(0)
self.guesses.append(word) #Add this guess to a list for posterity
self.guess_count += 1 #I debated where in the chain to put this. I landed here for clarity and consistency
if word == self.game_word:
print("You win! You found the word '{}' in {} guesses".format(self.game_word,self.guess_count))
return answer
Now that we have our guess and its score, we need to reevaluate the guessing pool.
def re_evaluate(self,answer):
word = self.guesses[-1] #okay, not just for posterity, but we need to compare the guess word's letters against the numeric answer from 'guess'
for i,code in enumerate(answer):
letter = word[i]
start = len(self.guess_words)
if code == 2:
self.correct_position[i] = letter #
self.letters_in.add(letter)
self.guess_words = [w for w in self.guess_words if (w[i] == letter)]
#We replace the guessing pool with this list comprehension
#Condition if words have matched letter in matched position
elif code == 1:
self.letters_in.add(letterl)
self.guess_words = [w for w in self.guess_words if ((letter in w) and (w[i] is not letter))]
#We replace the guessing pool with this list comprehension
#Condition if words have matched letter in the word, but NOT in that matched position
else:
self.letters_out.add(letter)
self.guess_words = [w for w in self.guess_words if (letter not in w)]
#We replace the guessing pool with this list comprehension
#Condition if words do NOT have the matched letter
self.analyze() # rescore the scoring dicts
This is the easy part. It's already done above by the call to self.analyze()
To repeat this process automatically we need to simulate playing the game.
def self_test(self, word_to_play, method="sc_prod"):
self.set_word(word_to_play)
while True:
s = self.suggest(method)
if len(s) == 0:
print('failed on word ', self.game_word)
choice = s[0]
g = self.guess(choice)
self.re_evaluate(g)
if (choice == self.game_word) or (self.guess_count >= 6):
break
won = True if self.guesses[-1] == self.game_word else False
performance = {
"won":won,
"attempts":self.guess_count,
}
return performance
#Collins Scrabble Words 2019
with open('CSW2019.txt') as file:
all_words = file.read().lower().splitlines()
all_words = all_words[2:]
all_fives = [word for word in all_words if len(word) == 5]
import random
import statistics
import math
class wordle_game:
def __init__(self, dictionary, word_length=5):
self.word_length = word_length
self.available_words = [word for word in dictionary if len(word) == self.word_length]
self.guess_words = self.available_words.copy() # because I know I want to reduce this while keeping the original intact
#now here is what we need for scoring:
self.all_letters = []
# this list will contain _every_ letter in every five letter word in the english dictionary.
#is this efficeint? no. But do I care? not yet. First things first
self.global_letters_count = 0
#number of all letters. I could sum() the all_letters, but for now I want to add as I go later
self.global_letters = dict()
#keys will be letters a-z
self.local_letters = [dict() for i in range(self.word_length)]
self.local_letters_count = [0 for i in range(self.word_length)]
#Make a dict for each slot (one for each five letters)
#These dicts will contain letters a-z for each slot
#Prepare to tally the sum of entries per slot
self.guess_count = 0
self.guesses = list()
self.correct_position = [0 for i in range(self.word_length)]
self.letters_in = set()
self.letters_out = set()
self.analyze()
def analyze(self):
self.count_letters()
self.letter_share()
self.score_words()
def count_letters(self):
for word in self.guess_words: #this is the copy of dictionary above. It will modify as we eliminate words
for i,l in enumerate(word): #get each letter one at a time
self.all_letters.append(l) #this will add all letters to above list
if l not in self.global_letters.keys():
self.global_letters[l] = {'count':0,'share':0} #add each letter to global dict
self.global_letters[l]['count'] += 1
self.global_letters_count += 1
if l not in self.local_letters[i].keys(): #now we use i to determin slot in word
self.local_letters[i][l] = {'count':0,'share':0}
self.local_letters[i][l]['count'] += 1
self.local_letters_count[i] += 1
def letter_share(self):
for l in self.global_letters.keys():
self.global_letters[l]['share'] = self.global_letters[l]['count']/self.global_letters_count
#We are dividing the total number of occurences of each letter by all letters ever used
#I call this 'share'. It represents the percentage or share each letter gets globally
for i,letter_dict in enumerate(self.local_letters):
for l in letter_dict.keys():
letter_dict[l]['share'] = letter_dict[l]['count']/self.local_letters_count[i]
#I find the share of each letter in each slot by its slot count
def score_words(self):
self.words_by_score = dict() #I don't like making class attributes in a method. but I also want to reset it each time.
self.score_by_letter(self.words_by_score,self.guess_words) #this seems redundant. But I'm going to add to this later
def score_by_letter(self, scoring_dict, word_dict):
for word in word_dict:
local_score = 0
global_score = 0
for i,letter in enumerate(word):
local_score += self.local_letters[i][letter]['share']
#We are summing the frequency of letter usage in each local position
for letter in set(word):
global_score += self.global_letters[letter]['share']
#We are summing the frequency of each letter usage globally
sc_added = local_score + global_score
sc_prod = local_score * global_score
sc_sq_added = local_score**2 + global_score**2
sc_sq_prod = local_score**2 * global_score**2
sc_loc_to_glob = local_score / global_score
sc_glob_to_loc = global_score / local_score
scoring_dict[word]={
'local':local_score,
'global':global_score,
'sc_added':sc_added,
'sc_prod':sc_prod,
'sc_sq_added':sc_sq_added,
'sc_sq_prod':sc_sq_prod,
'sc_loc_to_glob':sc_loc_to_glob,
'sc_glob_to_loc':sc_glob_to_loc
}
def suggest(self,method="sc_prod"):
suggestions = self.top_words(self.words_by_score, method,10)
return suggestions
def top_words(self,word_dict,method,n=10):
sorted_words = sorted(word_dict, key=lambda x: (word_dict[x][method]),reverse=True)
top_n = sorted_words[:n]
return top_n
def set_word(self, word_to_use):
self.game_word = word_to_use
def guess(self, word):
word = word.lower()
answer = []
#We are going to replicate the Wordle scoring.
# 0 == gray ; 1 == yellow ; 2 == green
for i,letter in enumerate(word):
if letter == self.game_word[i]:
answer.append(2)
elif letter in self.game_word:
answer.append(1)
else:
answer.append(0)
self.guesses.append(word) #Add this guess to a list for posterity
self.guess_count += 1 #I debated where in the chain to put this. I landed here for clarity and consistency
if word == self.game_word:
pass
#print("You win! You found the word '{}' in {} guesses".format(self.game_word,self.guess_count))
return answer
def re_evaluate(self,answer):
word = self.guesses[-1] #okay, not just for posterity, but we need to compare the guess word's letters against the numeric answer from 'guess'
for i,code in enumerate(answer):
letter = word[i]
start = len(self.guess_words)
if code == 2:
self.correct_position[i] = letter
self.letters_in.add(letter)
self.guess_words = [w for w in self.guess_words if (w[i] == letter)]
#We replace the guessing pool with this list comprehension
#Condition if words have matched letter in matched position
elif code == 1:
self.letters_in.add(letter)
self.guess_words = [w for w in self.guess_words if ((letter in w) and (w[i] is not letter))]
#We replace the guessing pool with this list comprehension
#Condition if words have matched letter in the word, but NOT in that matched position
else:
self.letters_out.add(letter)
self.guess_words = [w for w in self.guess_words if (letter not in w)]
#We replace the guessing pool with this list comprehension
#Condition if words do NOT have the matched letter
self.analyze() # rescore the scoring dicts
def self_test(self, word_to_play, method="sc_prod"):
self.set_word(word_to_play)
while True:
s = self.suggest(method)
if len(s) == 0:
print('failed on word ', self.game_word)
choice = s[0]
g = self.guess(choice)
self.re_evaluate(g)
if (choice == self.game_word) or (self.guess_count >= 6):
break
won = True if self.guesses[-1] == self.game_word else False
performance = {
"won":won,
"attempts":self.guess_count,
}
return performance
Outside our class we can cyle through all available words to see how good our program is at guessing all words within 6 tries
methods = {
'local':{'wins':0,'attempts':0},
'global':{'wins':0,'attempts':0},
'sc_added':{'wins':0,'attempts':0},
'sc_prod':{'wins':0,'attempts':0},
'sc_sq_added':{'wins':0,'attempts':0},
'sc_sq_prod':{'wins':0,'attempts':0},
'sc_loc_to_glob':{'wins':0,'attempts':0},
'sc_glob_to_loc':{'wins':0,'attempts':0}
}
total_wins = 0
testing_words = all_fives[:1000]
for method in methods.keys():
print("working on ",method)
for word in testing_words:
wordle_test = wordle_game(all_fives)
outcome = wordle_test.self_test(word,method)
if outcome['won']:
methods[method]['wins'] += 1
methods[method]['attempts'] += outcome['attempts']
for method in methods:
accuracy = methods[method]['wins']/len(testing_words)
av_attempts = methods[method]['attempts']/methods[method]['wins']
result = f"Method <{method}> wins {round(accuracy,3)*100}% with average {round(av_attempts,2)} attempts"
print(result)
This iterates through the first thousand words of all_words to give us a sample of accuracy. The above test returns the results:
Method < local > wins 92.3% with average 4.51 attempts
Method < global > wins 90.3% with average 4.18 attempts
Method < sc_added > wins 93.6% with average 4.39 attempts
Method < sc_prod > wins 93.7% with average 4.36 attempts
Method < sc_sq_added > wins 92.9% with average 4.44 attempts
Method < sc_sq_prod > wins 93.7% with average 4.36 attempts
Method < sc_loc_to_glob > wins 53.0% with average 5.26 attempts
Method < sc_glob_to_loc > wins 92.1% with average 4.41 attempts
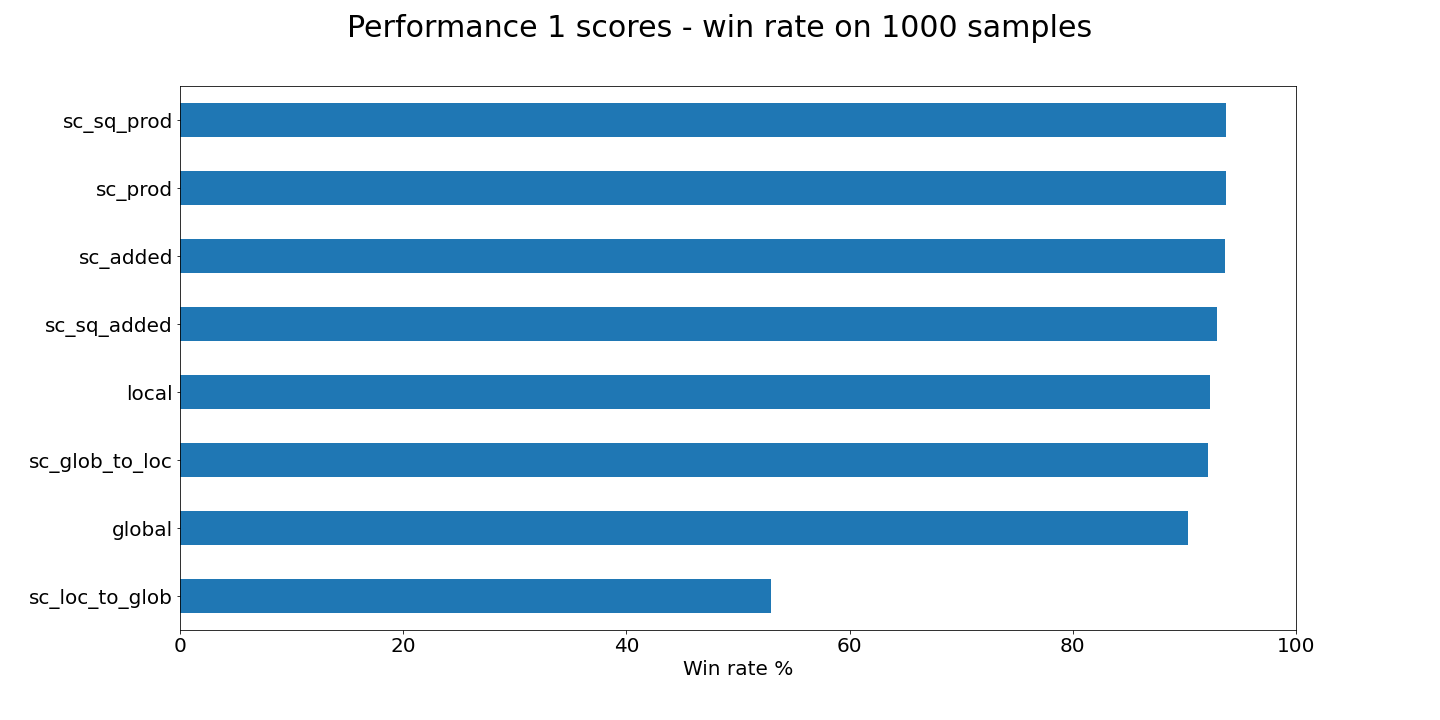
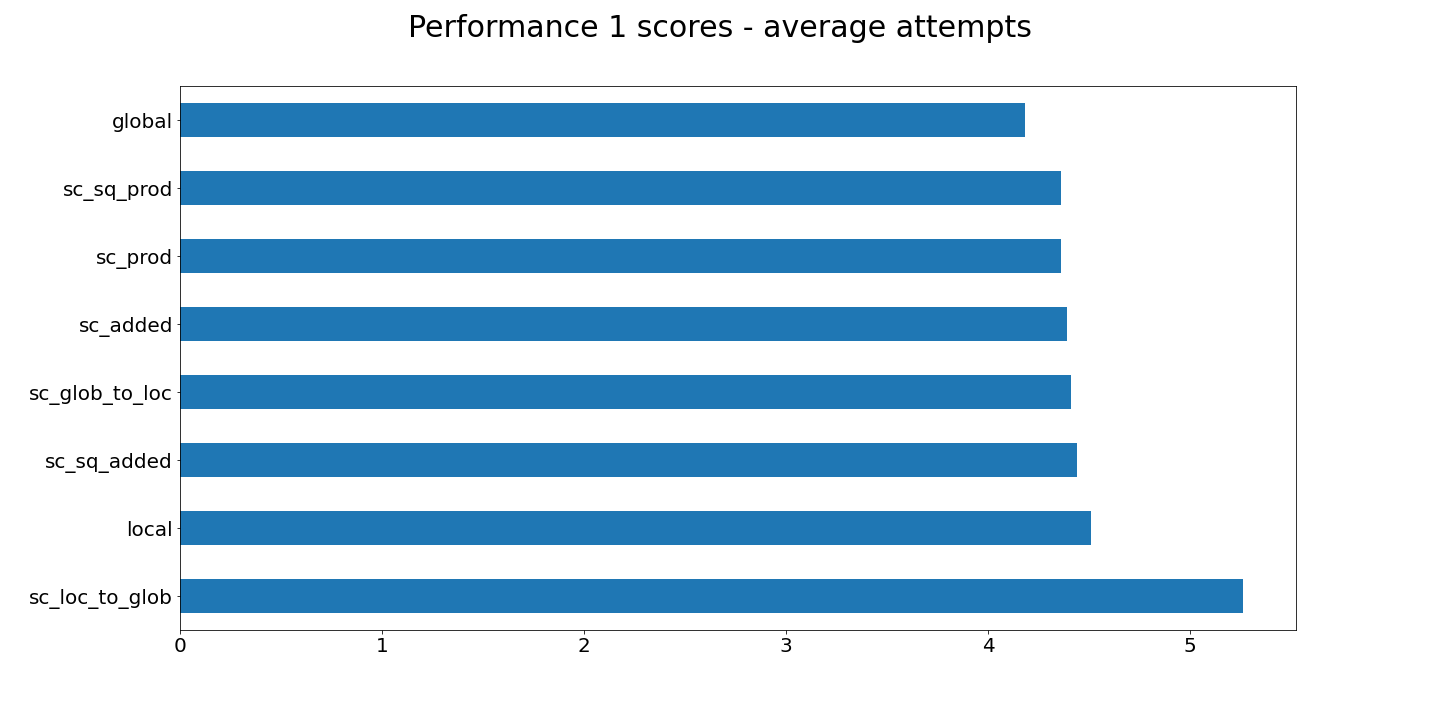
The above scores are not good enough. Our goal is 100% accuracy on all words. But we need to figure out how to get things in the 99% range to consider ourselves close. Remember, we have thousands of words on the table. So what can we do to improve things? Here's a few options:
I knew that the wordle creator used a custom dictionary of 2300 words. The closest I could find is a common words dictionary of about 1300 five letter words. Not good enough for production, but maybe it will improve things.
#Google-10000-english
with open('google-10000-english-usa-no-swears.txt') as commons:
common_words = commons.read().splitlines()
common_fives = [w for w in common_words if len(w) ==5]
At this point it will be easier to show the fill method, and then return to where to implement the commons dictionary.
We will add the common_fives dictionary as default commons attribe at __init__. We will also add the default fill attribute now. But if we are filling slots that have already been guessed, then we need a separate dictionary pool that is filtered differently from the actual guessing pool.
def __init__(self, dictionary=all_fives, commons=common_fives, fill=True, word_length=5):
...
...
...
self.commons = commons
self.fill = fill
self.fill_words = self.available_words.copy()
We will see the difference in the fill scores by scoring the fill_dictionary on its own words. At first it will be the same, but as words are guessed the based dicitonary will contain different words.
def score_words(self):
self.words_by_score = dict()
self.score_by_letter(self.words_by_score,self.guess_words)
self.fill_by_score = dict() #added
self.score_by_letter(self.fill_by_score,self.fill_words) #added
Now we are making use of both supplied parameters to score_by_letter(self, scoring_dict, word_dict). No additional changes need to be made to the scoring process.
But when are we going to implement the fill method? We will call it given game conditions:
So after some testing, I landed with:
We place this gate at the suggest() method.
def suggest(self,method="sc_prod"):
if (len(self.letters_in) < 6) and (len(self.guess_words) > 1) and (len(self.fill_words)>0) and (self.fill):
suggestions = self.top_words(self.fill_by_score,method,10)
else:
suggestions = self.top_words(self.words_by_score, method,10)
return suggestions
Now we have to update the fill_dictionary based on guesses. Remember, our goal with the fill method is to guess available letters in slots which have been knocked out in the guess_dictionary. This will give us the ability to wittle down global letters in fewer guesses. I went through lots of versions of this, including replicating the fill_dictionary from the guess_dictionary each round, or duplicating the word reductions on each code condition. In the end, I chose to filter the fill_dictionary once at the end of each letter guess.
def re_evaluate(self, answer):
...
for i,code in enumerate(answer):
letter = word[i]
...
...
self.fill_words = [w for w in self.fill_words if letter not in w]
By filtering out words which do not have the letter in the whole word, we are only keeping words with unique letters not so far guessed at all, giving us a completely unique filter pool for next suggestion. We can then guess from those new letters next time until we meet our fill criteria.
Now, let me show you where we put the commons dictionary bias.
def suggest(self,method="sc_prod"):
if (len(self.letters_in) < 6) and (len(self.guess_words) > 1) and (len(self.fill_words)>0) and (self.fill):
suggestions = self.top_words(self.fill_by_score,method,10)
else:
suggestions = self.top_words(self.words_by_score, method,10)
### Adding commons bias here ###
for word in reversed(suggestions): #reversed to preserve scored order after poping and re-adding
if word in self.commons:
suggestions.insert(0,suggestions.pop(suggestions.index(word)))
return suggestions
I am calling the commons a bias. If one of the top suggested words is in the common dictionary, there is a higher likelyhood that that word may actually be the real answer. And if it is already in the top options, we are probably not losing a lot of score value by choosing it over the default top scored word
From the returned list of of suggestions, mayby the top word is not the absolute best. Now, this method runs a little contrary to the commons bias, so we are not necessarily expecting the two hyperparameters to work super well together. But this may give us a sense of if the scoring method can be tailored better or if all the top scored words are equal.
We will put this randomizer in the self_test() method to filter its choice as returned from suggest().
def self_test(self, word_to_play, rand_guess=False, method='sc_prod')
...
...
#choice = s[0] ##former
choice = s[0] if not rand_guess else random.choice(s)
...
...
#Collins Scrabble Words 2019
with open('CSW2019.txt') as file:
all_words = file.read().lower().splitlines()
all_words = all_words[2:]
all_fives = [word for word in all_words if len(word) == 5]
#Google-10000-english
with open('google-10000-english-usa-no-swears.txt') as commons:
common_words = commons.read().splitlines()
common_fives = [w for w in common_words if len(w) ==5]
import random
import statistics
import math
class wordle_game:
def __init__(self, dictionary, commons=common_fives, fill=True, word_length=5):
self.word_length = word_length
self.available_words = [word for word in dictionary if len(word) == self.word_length]
self.guess_words = self.available_words.copy()
self.fill_words = self.available_words.copy() #added
self.commons = commons #added
self.fill = fill #added
self.all_letters = []
self.global_letters_count = 0
self.global_letters = dict()
self.local_letters = [dict() for i in range(self.word_length)]
self.local_letters_count = [0 for i in range(self.word_length)]
self.guess_count = 0
self.guesses = list()
self.correct_position = [0 for i in range(self.word_length)]
self.letters_in = set()
self.letters_out = set()
self.analyze()
def analyze(self):
self.count_letters()
self.letter_share()
self.score_words()
def count_letters(self):
for word in self.guess_words:
for i,l in enumerate(word):
self.all_letters.append(l)
if l not in self.global_letters.keys():
self.global_letters[l] = {'count':0,'share':0}
self.global_letters[l]['count'] += 1
self.global_letters_count += 1
if l not in self.local_letters[i].keys():
self.local_letters[i][l] = {'count':0,'share':0}
self.local_letters[i][l]['count'] += 1
self.local_letters_count[i] += 1
def letter_share(self):
for l in self.global_letters.keys():
self.global_letters[l]['share'] = self.global_letters[l]['count']/self.global_letters_count
for i,letter_dict in enumerate(self.local_letters):
for l in letter_dict.keys():
letter_dict[l]['share'] = letter_dict[l]['count']/self.local_letters_count[i]
def score_words(self):
self.words_by_score = dict()
self.score_by_letter(self.words_by_score,self.guess_words)
self.fill_by_score = dict() #added
self.score_by_letter(self.fill_by_score,self.fill_words) #added
def score_by_letter(self, scoring_dict, word_dict):
for word in word_dict:
local_score = 0
global_score = 0
for i,letter in enumerate(word):
local_score += self.local_letters[i][letter]['share']
for letter in set(word):
global_score += self.global_letters[letter]['share']
sc_added = local_score + global_score
sc_prod = local_score * global_score
sc_sq_added = local_score**2 + global_score**2
sc_sq_prod = local_score**2 * global_score**2
sc_loc_to_glob = local_score / global_score
sc_glob_to_loc = global_score / local_score
scoring_dict[word]={
'local':local_score,
'global':global_score,
'sc_added':sc_added,
'sc_prod':sc_prod,
'sc_sq_added':sc_sq_added,
'sc_sq_prod':sc_sq_prod,
'sc_loc_to_glob':sc_loc_to_glob,
'sc_glob_to_loc':sc_glob_to_loc
}
def suggest(self,method="sc_prod"):
if (len(self.letters_in) < 6) and (len(self.guess_words) > 1) and (len(self.fill_words)>0) and (self.fill): #added
suggestions = self.top_words(self.fill_by_score,method,10)
else:
suggestions = self.top_words(self.words_by_score, method,10)
for word in reversed(suggestions): #added
if word in self.commons: #added
suggestions.insert(0,suggestions.pop(suggestions.index(word))) #added
return suggestions
def top_words(self,word_dict,method,n=10):
sorted_words = sorted(word_dict, key=lambda x: (word_dict[x][method]),reverse=True)
top_n = sorted_words[:n]
return top_n
def set_word(self, word_to_use):
self.game_word = word_to_use
def guess(self, word):
word = word.lower()
answer = []
for i,letter in enumerate(word):
if letter == self.game_word[i]:
answer.append(2)
elif letter in self.game_word:
answer.append(1)
else:
answer.append(0)
self.guesses.append(word)
self.guess_count += 1
if word == self.game_word:
pass
#print("You win! You found the word '{}' in {} guesses".format(self.game_word,self.guess_count))
return answer
def re_evaluate(self,answer):
word = self.guesses[-1]
for i,code in enumerate(answer):
letter = word[i]
start = len(self.guess_words)
if code == 2:
self.correct_position[i] = letter
self.letters_in.add(letter)
self.guess_words = [w for w in self.guess_words if (w[i] == letter)]
elif code == 1:
self.letters_in.add(letter)
self.guess_words = [w for w in self.guess_words if ((letter in w) and (w[i] is not letter))]
else:
self.letters_out.add(letter)
self.guess_words = [w for w in self.guess_words if (letter not in w)]
self.fill_words = [w for w in self.fill_words if letter not in w] #added
self.analyze()
def self_test(self, word_to_play,rand_guess=False, method="sc_prod"):
self.set_word(word_to_play)
while True:
s = self.suggest(method)
if len(s) == 0:
print('failed on word ', self.game_word)
choice = s[0] if not rand_guess else random.choice(s) #Added/modified
g = self.guess(choice)
self.re_evaluate(g)
if (choice == self.game_word) or (self.guess_count >= 6):
break
won = True if self.guesses[-1] == self.game_word else False
performance = {
"won":won,
"attempts":self.guess_count,
}
return performance
Let's reset the Performance test to accomodate our changes. From the previous performance test, we see that our top scoring methods were:
Keep in mind that these accuracies change dramatically based on sample size of the performance test. We are only sampling on 1000 words right now. But in previous full tests, I have discovered that these still remain high/highest. So for our next test we will use the 'sc_prod' scoring method. Also keep in mind that we are, right now, taking the first 1000 words from our all_fives dictionary. This means the next scores can compare with the previous, because they are testing on the same words. Later we could use a randomizer to sample if the full list is too much.
hypers = {
"sc_prod + commons":{'methods':{'score':'sc_prod','commons':True,'fill':False,'random':False},'wins':0,'attempts':0},
"sc_prod + commons + fill":{'methods':{'score':'sc_prod','commons':True,'fill':True,'random':False},'wins':0,'attempts':0},
"sc_prod + commons + random":{'methods':{'score':'sc_prod','commons':True,'fill':False,'random':True},'wins':0,'attempts':0},
"sc_prod + commons + fill + random":{'methods':{'score':'sc_prod','commons':True,'fill':True,'random':True},'wins':0,'attempts':0},
"sc_prod + fill":{'methods':{'score':'sc_prod','commons':False,'fill':True,'random':False},'wins':0,'attempts':0},
"sc_prod + fill + random":{'methods':{'score':'sc_prod','commons':False,'fill':True,'random':True},'wins':0,'attempts':0},
"sc_prod + random":{'methods':{'commons':False,'fill':False,'random':True},'wins':0,'attempts':0},
}
testing_words = all_fives[:1000]
for hyper in hypers.keys():
method = hypers[hyper]['methods']['score']
commons = common_fives if hypers[hyper]['methods']['commons'] else []
fill = hypers[hyper]['methods']['fill']
rand = hypers[hyper]['methods']['random']
print("working on ",hyper)
for word in testing_words:
wordle_test = wordle_game(all_fives, commons, fill)
outcome = wordle_test.self_test(word,rand_guess=rand, method=method)
if outcome['won']:
hypers[hyper]['wins'] += 1
hypers[hyper]['attempts'] += outcome['attempts']
for hyper in hypers:
accuracy = hypers[hyper]['wins']/len(testing_words)
av_attempts = hypers[hyper]['attempts']/hypers[hyper]['wins']
result = f"Method <{hyper}> wins {round(accuracy*100,3)}% with average {round(av_attempts,2)} attempts"
print(result)
The above test returns the results:
Method
Method
Method
Method
Method
Method
Method
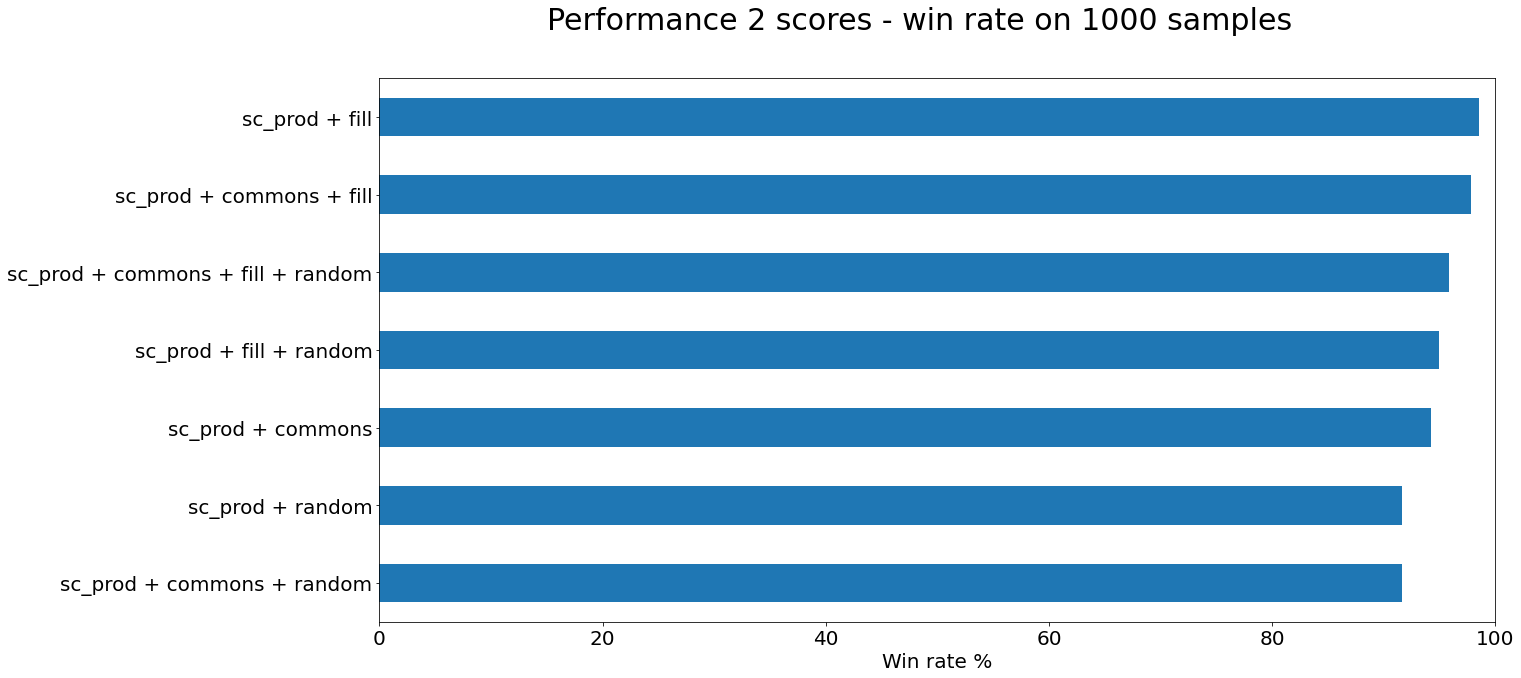
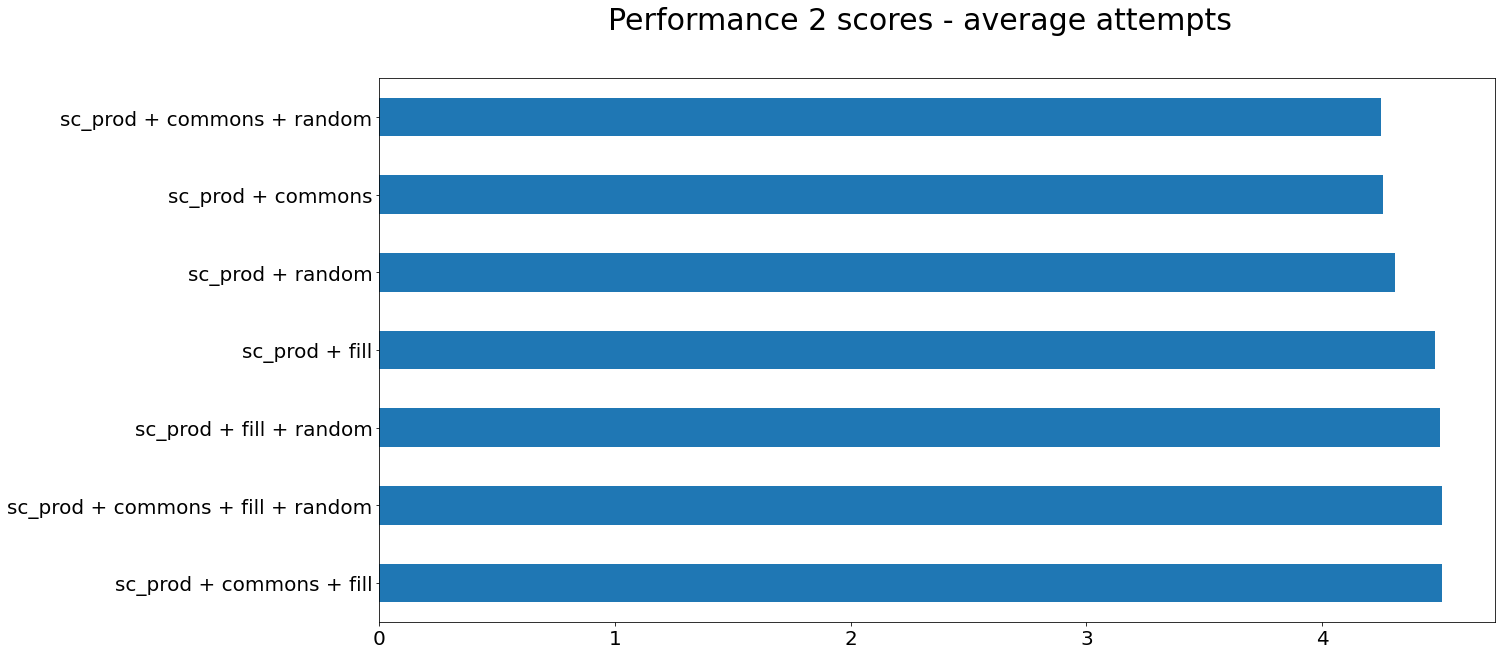
Now we are beginning to see some decent results. Keep in mind this is only with a small sample. But some of these hyperparameters do increase guessing accuracy. Of note are
| hyperparameter | accuracy |
|---|---|
| fill | 98.5% |
| fill with commons | 97.8% |
| fill with commons and random | 95.8% |
The program is now starting to take shape, now that we have our best performer within 1.5% of perfection (on small sample). I realize at this point that the dictionary I'm pulling from is too large. Using the commons method didn't overperform the basic fill method. Then again, we are trying to guess every word in the all_words dictionary, while our commons dictionary is too small to play Wordle. So our first solution must be to provide a more accurate dictionary for our program to train on.
This is the point at which someone might be tempted throw out the hack word. The best possible dictionary(s) to use are obsviously the source code dictionaries. Incredably, the list of all acceptable words (comparable to our all_words) and the list of guessing words (comparable to our commons) is available in the client side of Wordle. Now, this is as of the last week of January 2022. New aquisitions could obviously change what is available. But I doubt the source dictionaries themselves will change much. If they update new words to include (say, based on new popular slang), then we will need to add them. But right now, I expect this to function for the duration of this Wordle iteration.
I downloaded the .js file served by Wordle servers. Inside a mostly minified javascript, a Mount Everest of words rises after scrolling. I copied the two lists and turned them into \n deliniated txt files.
To clarify, the two arrays provided in the source code put together essentially represent our condensed five-word list from the Collins Scrabble dictionary. From that massive list, the Wordle creators pulled out about 2300 to be options for answers. They still allow guesses from the full list.
So, we will load both lists, keep the smaller 2300 list separate, and then combine them as a new all_words dictionary. These will replace our previous all_words and commons dictionary. Exept now we know for sure the commons will contain the correct answer.
#Wordle source code
with open('source_list_all_words.txt') as file:
all_fives = file.read().splitlines()
#Wordle source code
with open('source_list.txt') as file:
true_fives = file.read().splitlines()
all_source_words = [*all_fives, *true_fives]
Now we need to change around the way our class receives and stores the dictionaries. And, since we have no intent at this point of changing the five letter rule, we will drop that option and use range(5) and 5 when needed. Finally, since we only need to call the method once then we can place it as an __init__ attribute.
def __init__(self, full_dictionary, true_dictionary, commons=True, method='sc_prod', fill=True):
self.available_words = true_dictionary #changed
self.full_words = full_dictionary #changed
self.true_words = true_dictionary #added
self.commons = true_dictionary if commons else [] #changed
self.guess_words = self.true_words.copy() #changed
self.fill_words = self.full_words.copy() #changed
self.method = method #added
self.fill = fill
self.all_letters = []
self.global_letters_count = 0
self.global_letters = dict()
self.local_letters = [dict() for i in range(5)] #changed
self.local_letters_count = [0 for i in range(5)] #changed
self.guess_count = 0
self.guesses = list()
self.correct_position = [0 for i in range(5)] #changed
self.letters_in = set()
self.letters_out = set()
self.analyze()
When we run our fill_words option on the entire full dictionary, there may be letters in those slots which simply do not exist in the true_fives slots. Odd letters placed in weird positions typically don't make it into common vernacular. Therefore we must add a validator to our score_by_letter() method.
def score_by_letter(self, scoring_dict, word_dict):
for word in word_dict:
local_score = 0
global_score = 0
for i,letter in enumerate(word):
if letter in self.local_letters[i].keys(): #added
local_score += self.local_letters[i][letter]['share']
if letter in self.global_letters.keys(): #added and changed
global_score += self.global_letters[letter]['share']
...
...
You may notice a shift in theory regarding the global letters. Before we were using the set(word) to eliminate duplicate letters from double dipping on the global score. Now lets open that up to see what we find.
At this point, won't it be interesting to see the difference in scoring all letters in the full dictionary verses scoring letters by only the words which might be answers?
To make it clear, what we are looking at is looking at letter share/frequency in all 5-letter words in english (the first charts), and now comparing to letter share/frequency to only words used as potential Wordle answers.


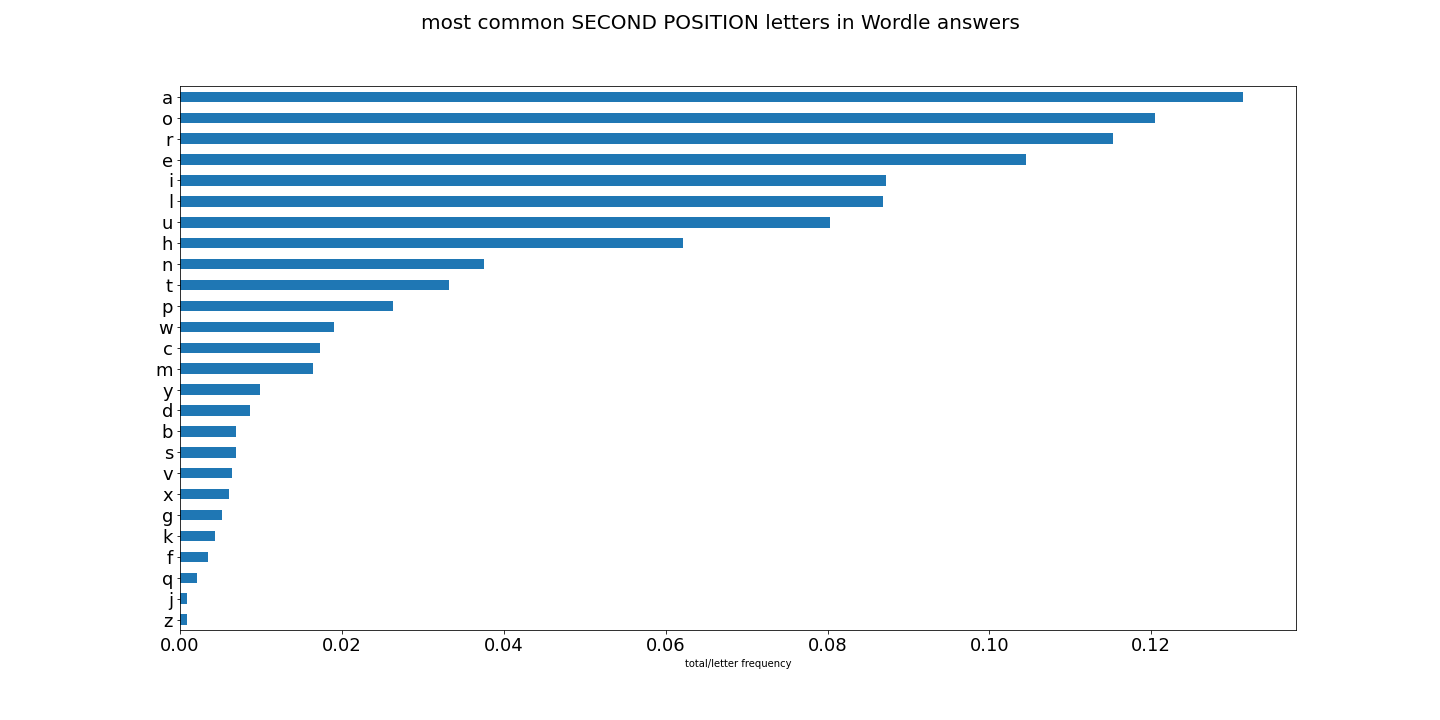
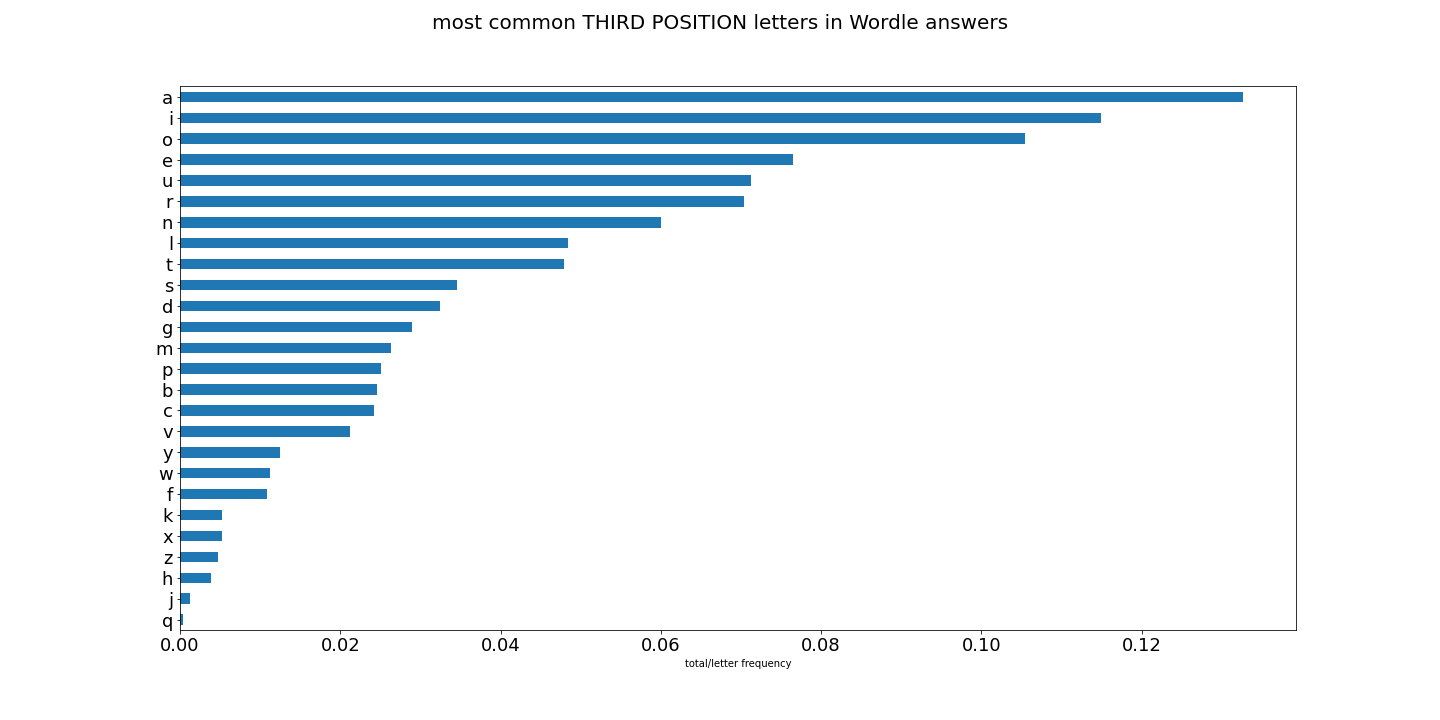
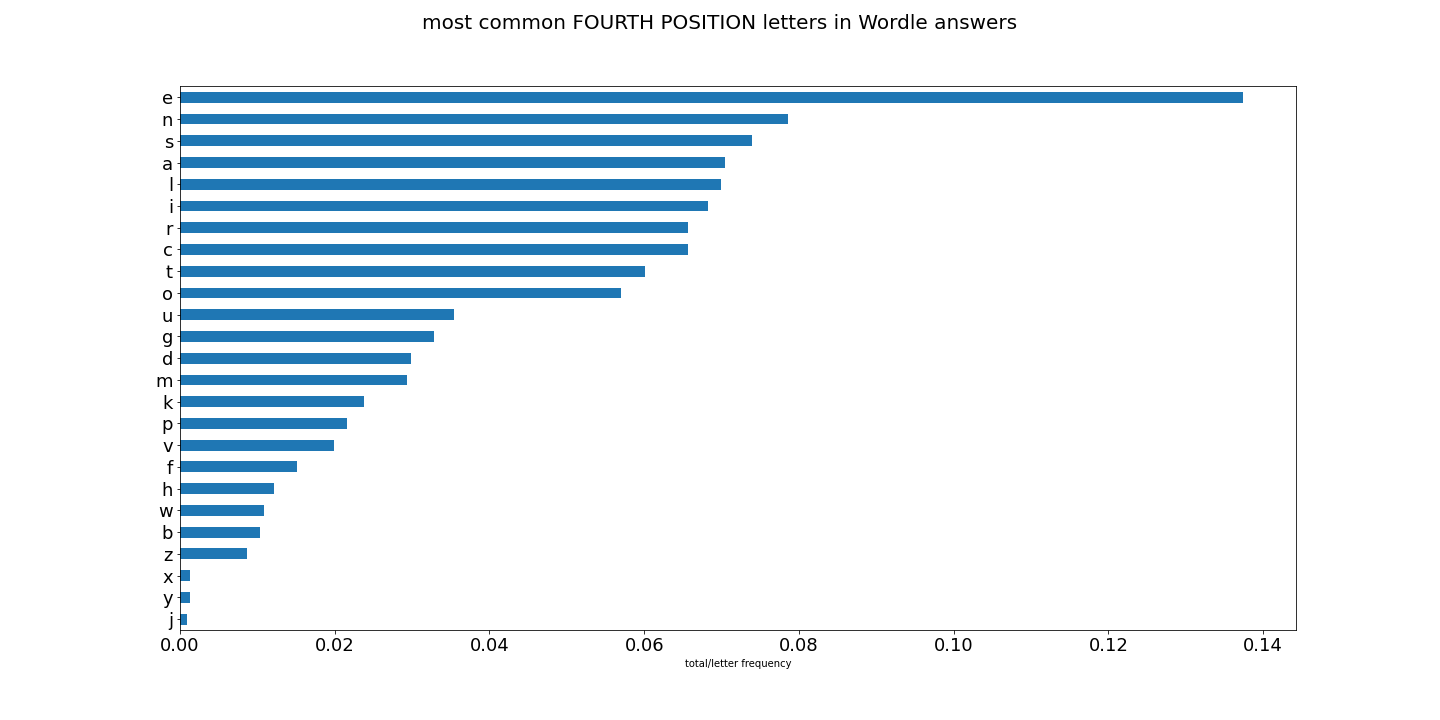
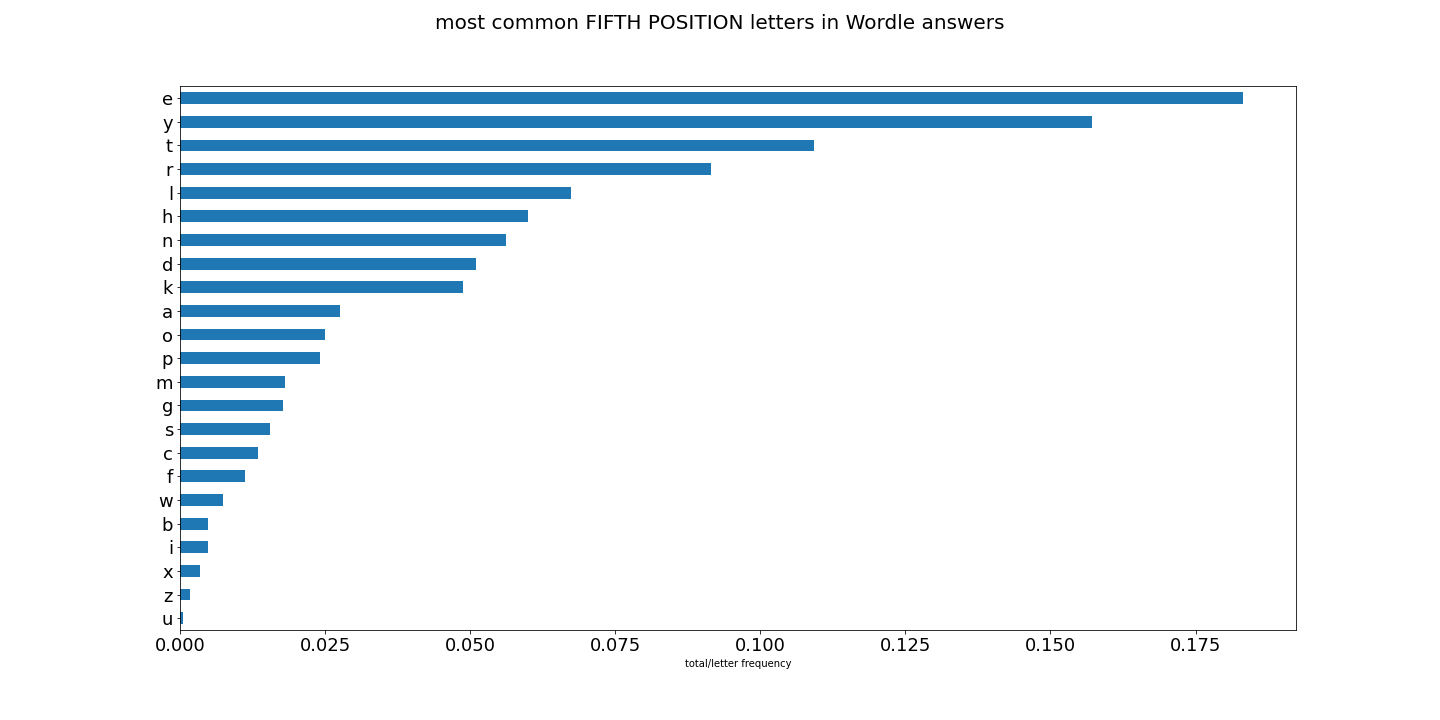
But lets see how they compare with the former all_words.
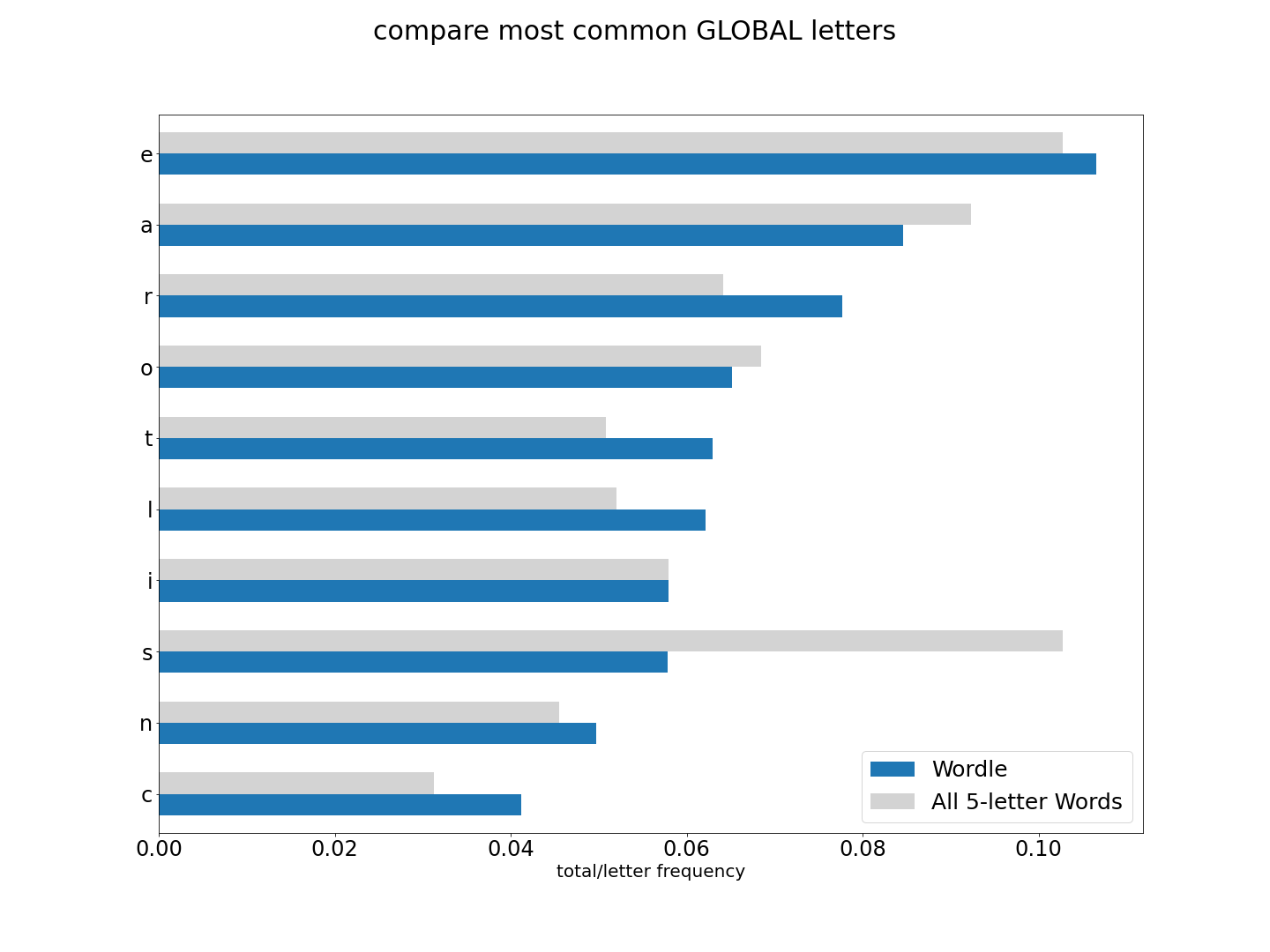
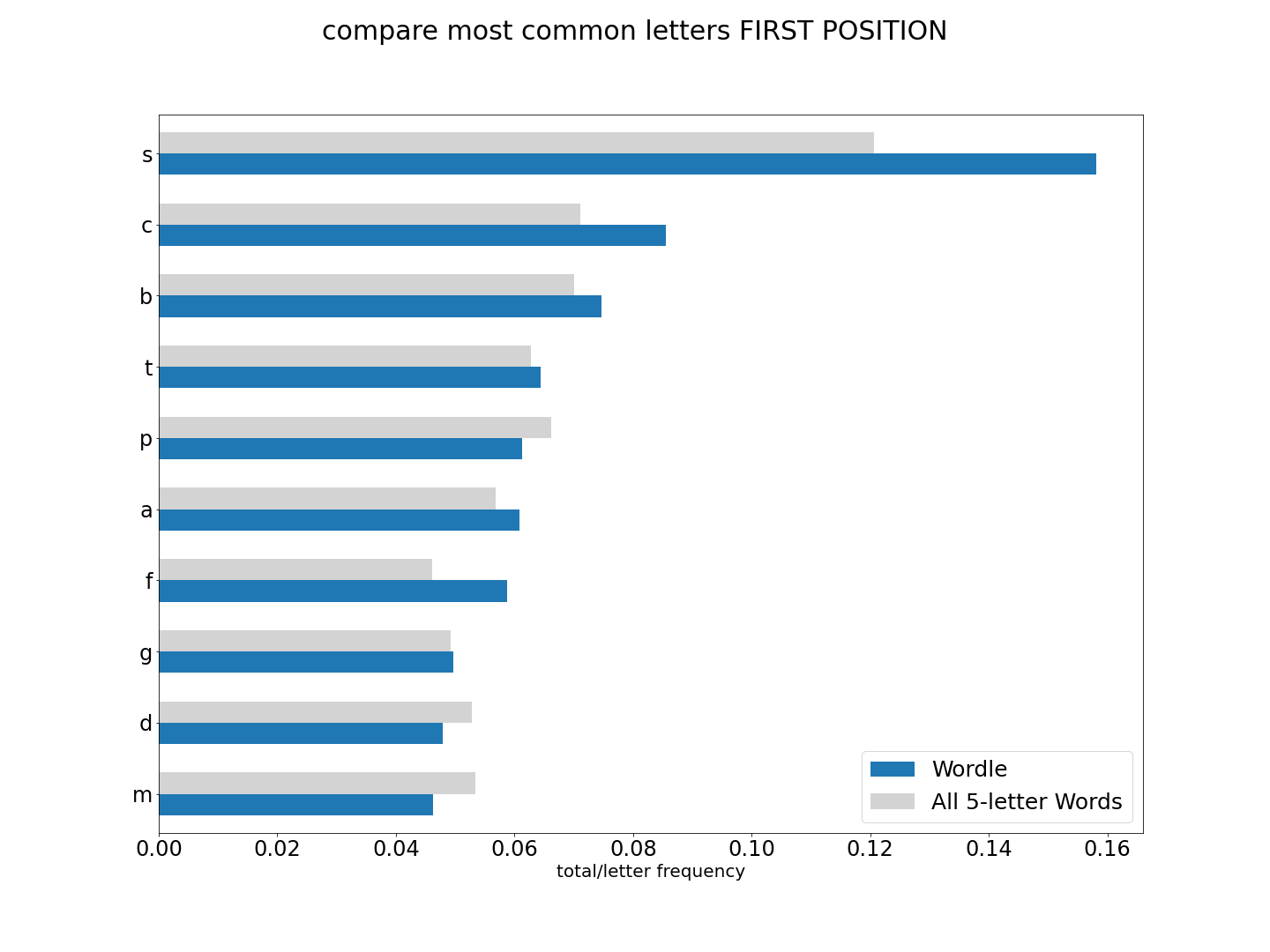
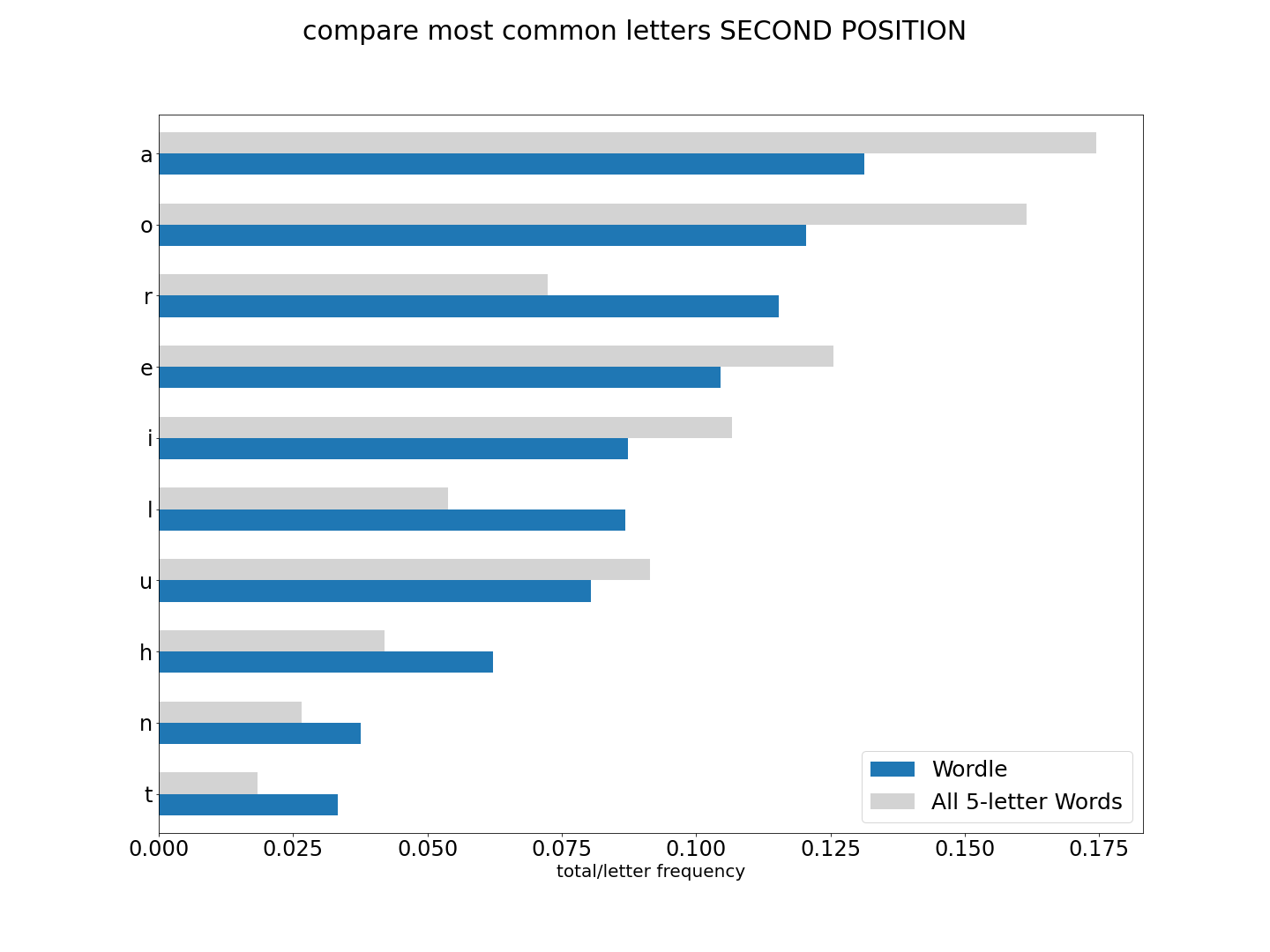
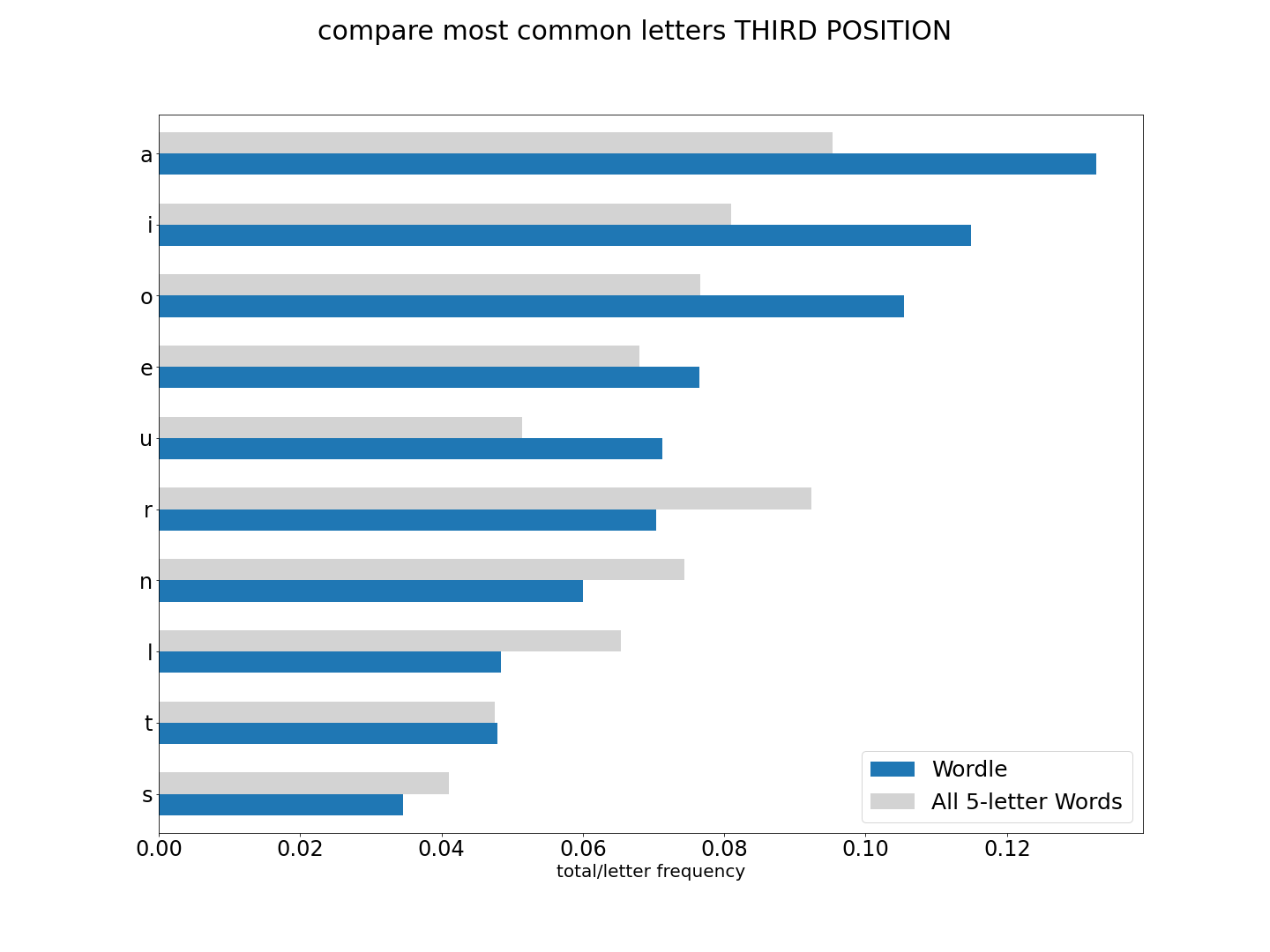
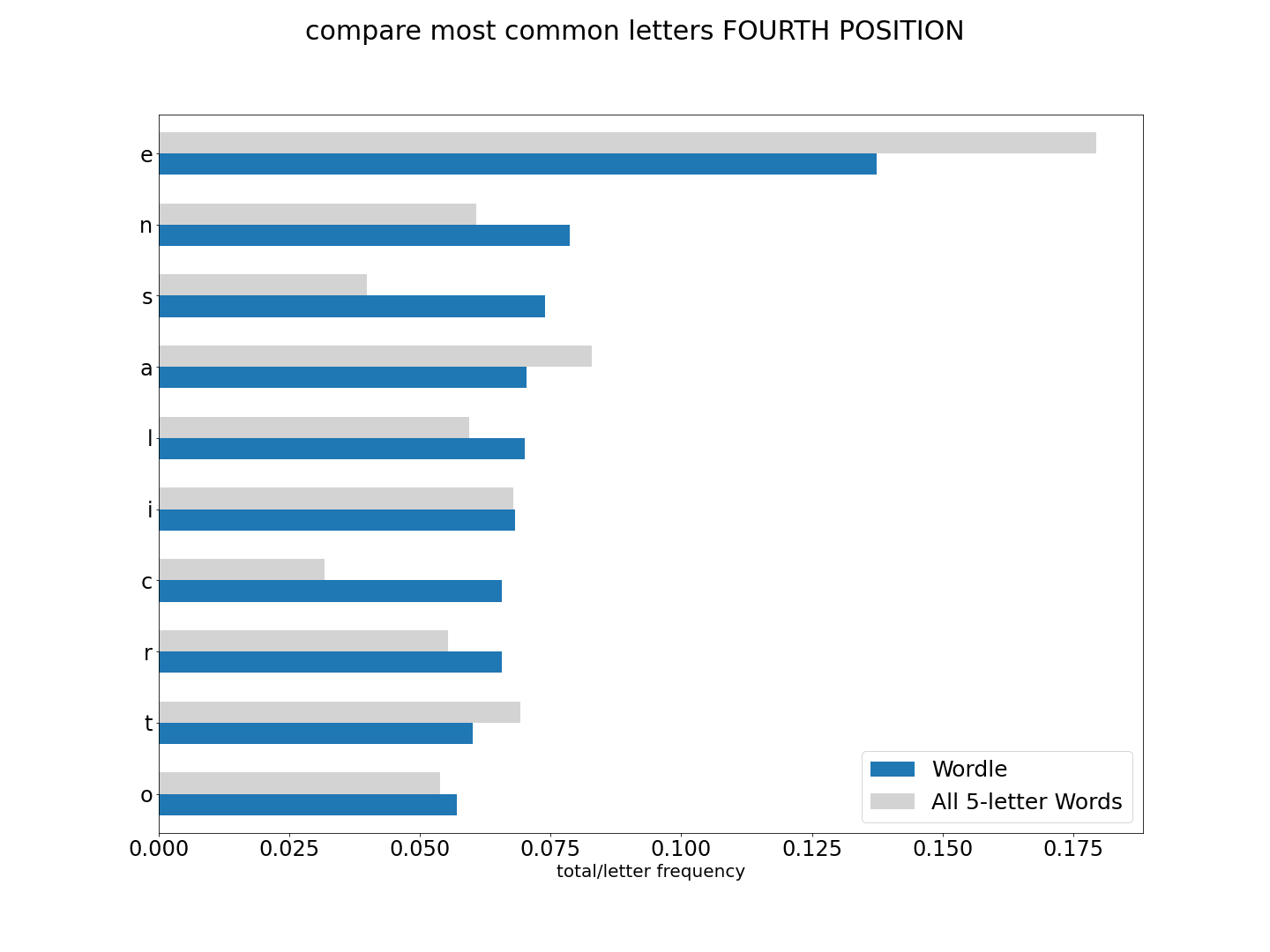
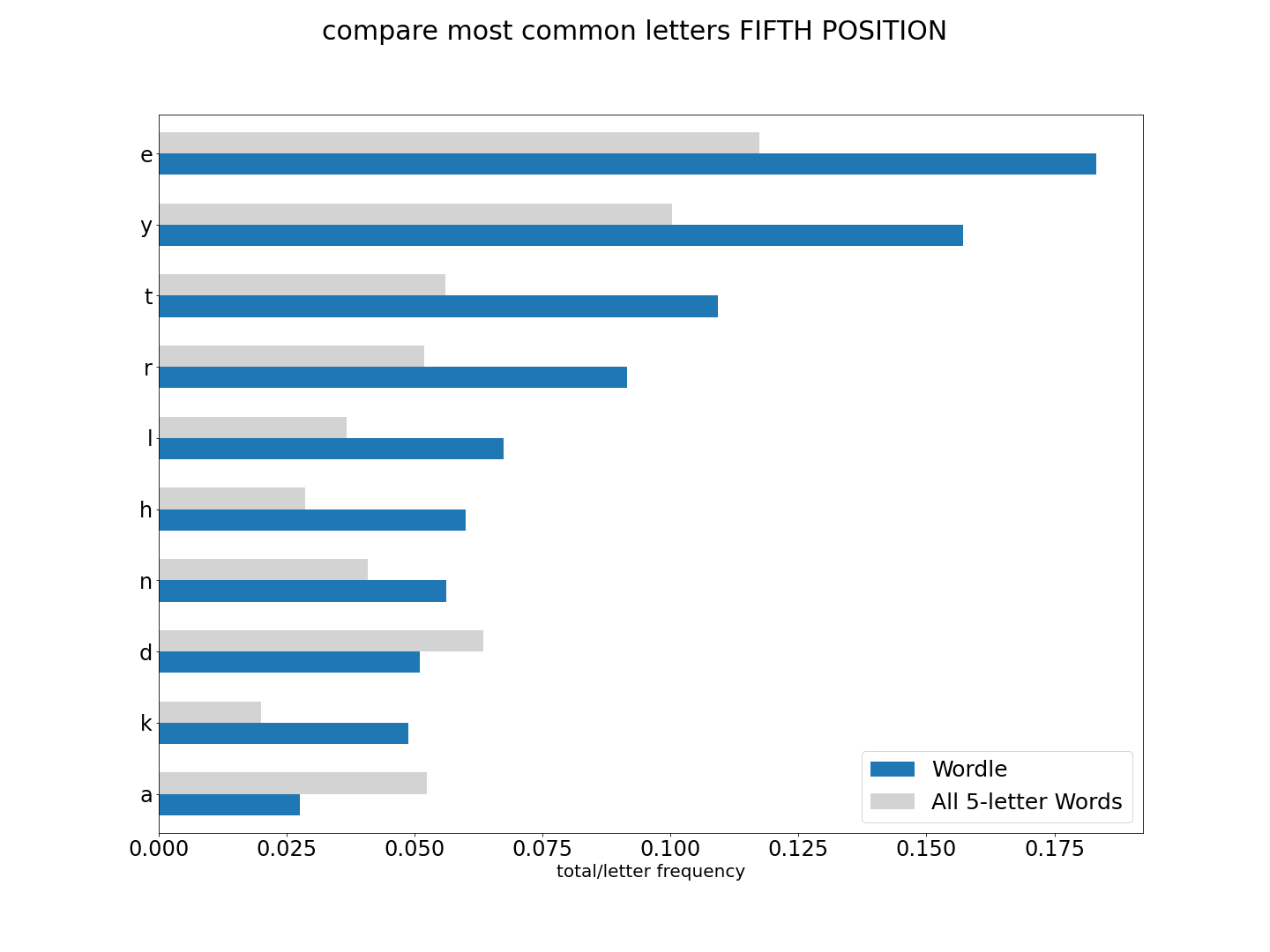
Since we have changed our approah a bit, we need to go back to our scoring methods to make sure things have improved both for our 'sc_prod' method, but also to see if any other method has excelled. Let's go though and add a few more, and take out a few that we know underperform.
Let's drop the 'sc_loc_to_glob' and 'sc_glob_to_loc'. And let's add in:
'set_score' : to replace the idea we had first with 'global'. This will score for letters that appear at least once per word.
'in_words' : the share of words who have this letter
'set_in_prod' : the product of 'set_score' and 'in_words'
'all_prod' : the product of all methods
We add some attributes to __init__
def __init__(self, *):
...
...
self.all_letters = []
self.global_letters_count = 0
self.global_letters = dict()
self.once_per_word_count = 0 #added
self.once_per_word = dict() #added
self.words_per_letter = dict() #added
...
...
And some adders in count_letters() and letter_share()
def count_letters(self):
for word in self.guess_words:
for i,l in enumerate(word):
...
...
for s in set(w): #added
if s not in self.once_per_word.keys():
self.once_per_word[s] = {'count':0,'share':0}
self.words_per_letter[s] = {'count':0,'share':0}
self.once_per_word[s]['count'] += 1
self.once_per_words_count += 1
self.words_per_letter[s]['count'] += 1
def letter_share(self):
...
...
for s in self.once_per_word.keys(): #added
self.once_per_word[s]['share'] = self.once_per_word[s]['count']/self.once_per_word_count
self.words_per_letter[s]['share'] = self.words_per_letter[s]['count']/len(self.guess_words)
Update the scoring dict in score_by_letter()
def score_by_letter(self, *):
for word in word_dict:
...
set_score = 0 #added
in_words_score = 0 #added
...
for l in set(word): #added
if l in self.once_per_word.keys():
set_score += self.once_per_word[l]['share']
in_words_score = self.words_per_letter[l]['share']
...
...
#sc_loc_to_glob = local_score / global_score #remove
#sc_glob_to_loc = global_score / local_score #remove
set_in_prod = set_score*in_words_score #added
all_prod = local_score*global_score*set_score*in_words_score #added
scoring_dict[word]={
...
...
#'sc_loc_to_glob':sc_loc_to_glob, #remove
#'sc_glob_to_loc':sc_glob_to_loc #remove
'set_score':set_score, #added
'in_words':in_words_score, #added
'set_in_prod':set_in_prod, #added
'all_prod':all_prod #added
#Wordle source code
with open('source_list_all_words.txt') as file:
all_fives = file.read().splitlines()
#Wordle source code
with open('source_list.txt') as file:
true_fives = file.read().splitlines()
all_source_words = [*all_fives, *true_fives]
import random
import statistics
import math
class wordle_game:
def __init__(self, full_dictionary, true_dictionary, commons=True, method="sc_prod", fill=True):
self.available_words = true_dictionary #changed
self.full_words = full_dictionary #changed
self.true_words = true_dictionary #added
self.commons = true_dictionary if commons else [] #changed
self.guess_words = self.true_words.copy() #changed
self.fill_words = self.full_words.copy() #changed
self.method = method
self.fill = fill
self.all_letters = []
self.global_letters_count = 0
self.global_letters = dict()
self.once_per_word_count = 0 #added
self.once_per_word = dict() #added
self.words_per_letter = dict() #added
self.local_letters = [dict() for i in range(5)] #changed
self.local_letters_count = [0 for i in range(5)] #changed
self.guess_count = 0
self.guesses = list()
self.correct_position = [0 for i in range(5)] #changed
self.letters_in = set()
self.letters_out = set()
self.analyze()
def analyze(self):
self.count_letters()
self.letter_share()
self.score_words()
def count_letters(self):
for word in self.guess_words:
for i,l in enumerate(word):
self.all_letters.append(l)
if l not in self.global_letters.keys():
self.global_letters[l] = {'count':0,'share':0}
self.global_letters[l]['count'] += 1
self.global_letters_count += 1
if l not in self.local_letters[i].keys():
self.local_letters[i][l] = {'count':0,'share':0}
self.local_letters[i][l]['count'] += 1
self.local_letters_count[i] += 1
for s in set(word): #added
if s not in self.once_per_word.keys():
self.once_per_word[s] = {'count':0,'share':0}
self.words_per_letter[s] = {'count':0,'share':0}
self.once_per_word[s]['count'] += 1
self.once_per_word_count += 1
self.words_per_letter[s]['count'] += 1
def letter_share(self):
for l in self.global_letters.keys():
self.global_letters[l]['share'] = self.global_letters[l]['count']/self.global_letters_count
for i,letter_dict in enumerate(self.local_letters):
for l in letter_dict.keys():
letter_dict[l]['share'] = letter_dict[l]['count']/self.local_letters_count[i]
for s in self.once_per_word.keys(): #added
self.once_per_word[s]['share'] = self.once_per_word[s]['count']/self.once_per_word_count
self.words_per_letter[s]['share'] = self.words_per_letter[s]['count']/len(self.guess_words)
def score_words(self):
self.words_by_score = dict()
self.score_by_letter(self.words_by_score,self.guess_words)
self.fill_by_score = dict()
self.score_by_letter(self.fill_by_score,self.fill_words)
def score_by_letter(self, scoring_dict, word_dict):
for word in word_dict:
local_score = 0
global_score = 0
set_score = 0 #added
in_words_score = 0 #added
for i,letter in enumerate(word):
if letter in self.local_letters[i].keys(): #added
local_score += self.local_letters[i][letter]['share']
if letter in self.global_letters.keys(): #added and changed
global_score += self.global_letters[letter]['share']
for l in set(word): #added
if l in self.once_per_word.keys():
set_score += self.once_per_word[l]['share']
in_words_score = self.words_per_letter[l]['share']
sc_added = local_score + global_score
sc_prod = local_score * global_score
sc_sq_added = local_score**2 + global_score**2
sc_sq_prod = local_score**2 * global_score**2
#sc_loc_to_glob = local_score / global_score #remove
#sc_glob_to_loc = global_score / local_score #remove
set_in_prod = set_score*in_words_score #added
all_prod = local_score*global_score*set_score*in_words_score #added
scoring_dict[word]={
'local':local_score,
'global':global_score,
'sc_added':sc_added,
'sc_prod':sc_prod,
'sc_sq_added':sc_sq_added,
'sc_sq_prod':sc_sq_prod,
#'sc_loc_to_glob':sc_loc_to_glob, #remove
#'sc_glob_to_loc':sc_glob_to_loc #remove
'set_score':set_score, #added
'in_words':in_words_score, #added
'set_in_prod':set_in_prod, #added
'all_prod':all_prod #added
}
def suggest(self,method="sc_prod"):
if not method:
method = self.method
if (len(self.letters_in) < 6) and (len(self.guess_words) > 1) and (len(self.fill_words)>0) and (self.fill):
suggestions = self.top_words(self.fill_by_score,method,10)
else:
suggestions = self.top_words(self.words_by_score, method,10)
for word in reversed(suggestions):
if word in self.commons:
suggestions.insert(0,suggestions.pop(suggestions.index(word)))
return suggestions
def top_words(self,word_dict,method,n=10):
sorted_words = sorted(word_dict, key=lambda x: (word_dict[x][method]),reverse=True)
top_n = sorted_words[:n]
return top_n
def set_word(self, word_to_use):
self.game_word = word_to_use
def guess(self, word):
word = word.lower()
answer = []
for i,letter in enumerate(word):
if letter == self.game_word[i]:
answer.append(2)
elif letter in self.game_word:
answer.append(1)
else:
answer.append(0)
self.guesses.append(word)
self.guess_count += 1
if word == self.game_word:
pass
#print("You win! You found the word '{}' in {} guesses".format(self.game_word,self.guess_count))
return answer
def re_evaluate(self,answer):
word = self.guesses[-1]
for i,code in enumerate(answer):
letter = word[i]
start = len(self.guess_words)
if code == 2:
self.correct_position[i] = letter
self.letters_in.add(letter)
self.guess_words = [w for w in self.guess_words if (w[i] == letter)]
elif code == 1:
self.letters_in.add(letter)
self.guess_words = [w for w in self.guess_words if ((letter in w) and (w[i] is not letter))]
else:
self.letters_out.add(letter)
self.guess_words = [w for w in self.guess_words if (letter not in w)]
self.fill_words = [w for w in self.fill_words if letter not in w]
self.analyze()
def self_test(self, word_to_play,rand_guess=False, method="sc_prod"):
self.set_word(word_to_play)
while True:
s = self.suggest(method)
if len(s) == 0:
print('failed on word ', self.game_word)
choice = s[0] if not rand_guess else random.choice(s)
g = self.guess(choice)
self.re_evaluate(g)
if (choice == self.game_word) or (self.guess_count >= 6):
break
won = True if self.guesses[-1] == self.game_word else False
performance = {
"won":won,
"attempts":self.guess_count,
}
return performance
For this, we will test on ALL wordle words len() = 2315
methods_hypers = {
"global + fill": {'methods':{'score':'global', 'commons':False, 'fill':True,'random':False},'wins':0,'attempts':0},
"global + fill + commons": {'methods':{'score':'global', 'commons':True, 'fill':True,'random':False},'wins':0,'attempts':0},
"sc_added + fill": {'methods':{'score':'sc_added', 'commons':False, 'fill':True,'random':False},'wins':0,'attempts':0},
"sc_added + fill + commons": {'methods':{'score':'sc_added', 'commons':True, 'fill':True,'random':False},'wins':0,'attempts':0},
"sc_prod + fill": {'methods':{'score':'sc_prod', 'commons':False, 'fill':True,'random':False},'wins':0,'attempts':0},
"sc_prod + fill + commons": {'methods':{'score':'sc_prod', 'commons':True, 'fill':True,'random':False},'wins':0,'attempts':0},
"sc_sq_added + fill": {'methods':{'score':'sc_sq_added', 'commons':False, 'fill':True,'random':False},'wins':0,'attempts':0},
"sc_sq_added + fill + commons": {'methods':{'score':'sc_sq_added', 'commons':True, 'fill':True,'random':False},'wins':0,'attempts':0},
"sc_sq_prod + fill": {'methods':{'score':'sc_sq_prod', 'commons':False, 'fill':True,'random':False},'wins':0,'attempts':0},
"sc_sq_prod + fill + commons": {'methods':{'score':'sc_sq_prod', 'commons':True, 'fill':True,'random':False},'wins':0,'attempts':0},
"set_score + fill": {'methods':{'score':'set_score', 'commons':False, 'fill':True,'random':False},'wins':0,'attempts':0},
"set_score + fill + commons": {'methods':{'score':'set_score', 'commons':True, 'fill':True,'random':False},'wins':0,'attempts':0},
"in_words + fill": {'methods':{'score':'in_words', 'commons':False, 'fill':True,'random':False},'wins':0,'attempts':0},
"in_words + fill + commons": {'methods':{'score':'in_words', 'commons':True, 'fill':True,'random':False},'wins':0,'attempts':0},
"set_in_prod + fill": {'methods':{'score':'set_in_prod', 'commons':False, 'fill':True,'random':False},'wins':0,'attempts':0},
"set_in_prod + fill + commons": {'methods':{'score':'set_in_prod', 'commons':True, 'fill':True,'random':False},'wins':0,'attempts':0},
"all_prod + fill": {'methods':{'score':'all_prod', 'commons':False, 'fill':True,'random':False},'wins':0,'attempts':0},
"all_prod + fill + commons": {'methods':{'score':'all_prod', 'commons':True, 'fill':True,'random':False},'wins':0,'attempts':0},
}
total_wins =0
testing_words = true_fives[:]
for hyper in methods_hypers.keys():
method = methods_hypers[hyper]['methods']['score']
commons = methods_hypers[hyper]['methods']['commons']
fill = methods_hypers[hyper]['methods']['fill']
rand = methods_hypers[hyper]['methods']['random']
print("working on ",hyper)
for word in testing_words:
wordle_test = wordle_game(all_source_words, true_fives, commons, fill)
outcome = wordle_test.self_test(word,rand_guess=rand, method=method)
if outcome['won']:
methods_hypers[hyper]['wins'] += 1
methods_hypers[hyper]['attempts'] += outcome['attempts']
for hyper in methods_hypers:
accuracy = methods_hypers[hyper]['wins']/len(testing_words)
av_attempts = methods_hypers[hyper]['attempts']/methods_hypers[hyper]['wins']
result = f"Method <{hyper}> wins {round(accuracy,6)}% with average {round(av_attempts,4)} attempts"
print(result)
Results:
Method < global + fill > wins 93.69% with average 4.9368 attempts
Method < global + fill + commons > wins 97.58% with average 4.6432 attempts
Method < sc_added + fill > wins 97.40% with average 4.5206 attempts
Method < sc_added + fill + commons> wins 98.53% with average 4.3012 attempts
Method < sc_prod + fill > wins 97.27% with average 4.5187 attempts
Method < sc_prod + fill + commons > wins 98.35% with average 4.4172 attempts
Method < sc_sq_added + fill > wins 97.32% with average 4.5193 attempts
Method < sc_sq_added + fill + commons > wins 97.88% with average 4.4925 attempts
Method < sc_sq_prod + fill > wins 97.27% with average 4.5187 attempts
Method < sc_sq_prod + fill + commons > wins 98.35% with average 4.4172 attempts
Method < set_score + fill > wins 99.39% with average 4.0561 attempts
Method < set_score + fill + commons > wins 99.04% with average 4.0462 attempts
Method < in_words + fill > wins 98.27% with average 4.6123 attempts
Method < in_words + fill + commons > wins 98.22% with average 4.6095 attempts
Method < set_in_prod + fill > wins 99.31% with average 4.0357 attempts
Method < set_in_prod + fill + commons > wins 99.09% with average 4.0179 attempts
Method < all_prod + fill > wins 98.40% with average 4.1471 attempts
Method < all_prod + fill + commons > wins 98.74% with average 4.1584 attempts
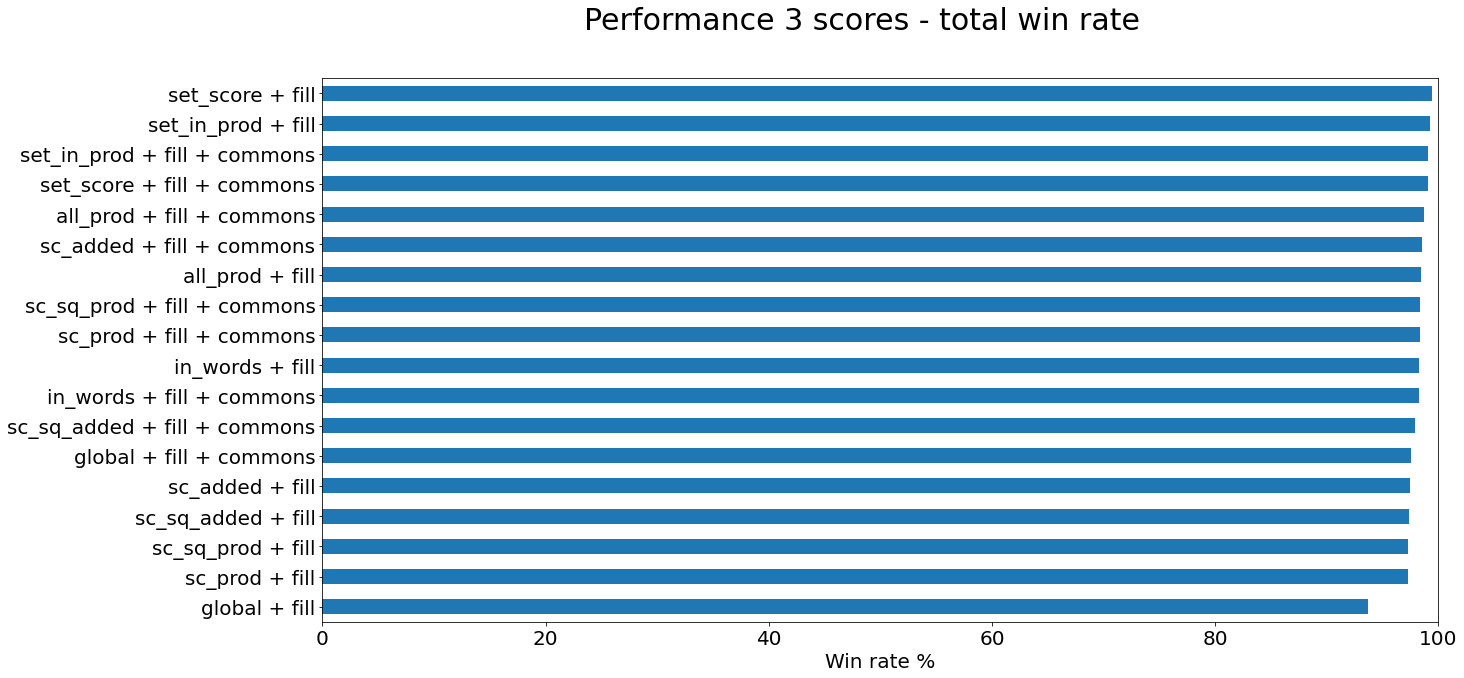
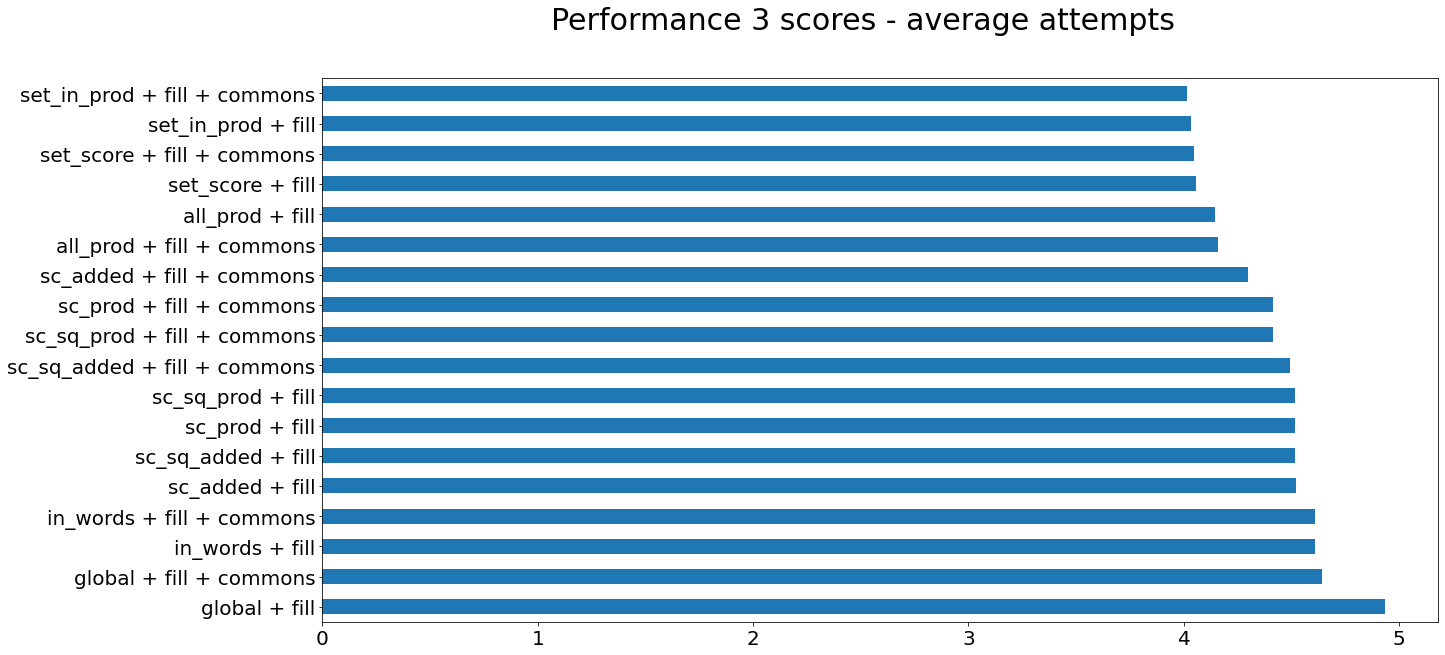
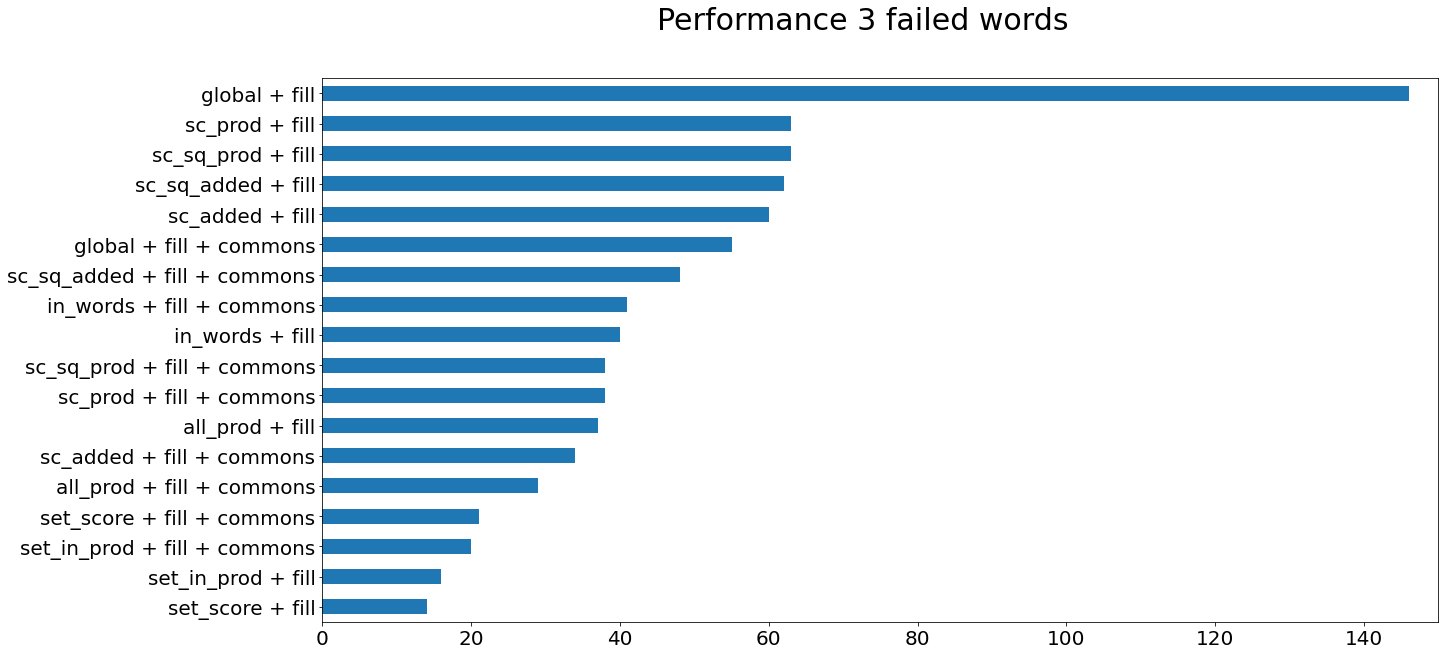
| method | hyper | accuracy | words failed |
|---|---|---|---|
| set_score | fill | 99.39% | 14 |
| set_in_prod | fill | 99.26% | 16 |
| sc_added | fill with commons | 98.53% | 34 |
Okay this is our last attempt to tune what we have before we need to try another approach. It just so happens that I will discover a better method due to this process below.
We currently have a 99.39% chance of beating Wordle every time. We have fourteen words we cannot yet win against. We need to find out why
To do that, lets take a look at what those words are. We will re-run the performance 3 test with the top two contenders. We will add their failed words to a list.
...
...
failed_words = dict()
for hyper in methods_hypers.keys():
failed_words[hyper] = []
...
...
for word in testing_words:
...
...
if outcome['won']:
...
else:
failed_words[hyper].append(word)
Failed words for 'set_score':
'alive',failed words for 'set_in_prod':
'gamer',
Since the two lists contain the shared words "stave" and "taunt" we will play the game manually to get the guess options prior to fail. I'll insert a print statment into the self_test() method.
After guess three on "stave" I have these words to choose from: ['waste', 'stage', 'stake', 'skate', 'taste', 'stave', 'state', 'baste']
And after the fourth guess: ['stage', 'stake', 'stave']
Unfortunately 'stave' would be guess seven.
After guess two on "taunt" I have these words: ['jaunt', 'chant', 'taunt', 'gaunt', 'haunt', 'daunt', 'vaunt']
Then ['jaunt', 'taunt', 'gaunt', 'daunt', 'vaunt']
Then ['jaunt', 'taunt', 'gaunt', 'daunt']
Can we reason why it comes to this? Well, our algorithm resets the scoring at each new collection of available words to pick. So when we get down to this size all it can do is return the top word of a list of words with almost identical letters. They would each have the similar enough scores to make the list ireducable. So what we need to do is isolate those unique letters before the fifth guess so that we can guess at least one more word using as many of those unique letters as possible. Maybe this will find that last letter before the last guess.
Let's work on a function which can identify unique letters and sort through all_source_words to find words that can match the most unique letters.
from collections import Counter
def find_unique(self, rate_of_occurence=1):
#count the letters in remaining guess_words
counted = Counter([l for word in self.guess_words for l in set(word)])
#make a list of letters that occur less than the rate_of_occurence parameter. In the above lists, we want default '1'
unique = [letter for letter,count in counted.items() if count <= rate_of_occurence]
# if there are no unique letters which meet threshold, return False
if len(unique) == 0:
return False
#prepare to find words which match most unique letters
top = dict()
for word in self.full_words:
#if we have a word which matches number of words, we don't need to look any farther
if len(unique) in top.keys():
break
matches = 0
for l in unique:
if l in word:
matches += 1
#if we have a word already with this number of matches, no need to add another
if matches in top.keys():
continue
#normally, we don't want words matched with only one unique letter. But if there actually is only one in unique, use it.
if matches > 1 or len(unique)==1:
top[matches] = [word]
#find biggest dict key. Return the word with the most unique letters
biggest_match = max(top.keys())
return top[biggest_match]
When and where are we going to implement this find_unique() method? First, we need to place a class attribute to turn this feature on or off. Let's call it 'safetynet'
def __init__(*, safetynet=0):
...
...
self.safetynet = safetynet #added
...
...
Where should we call the function? We need it to return a better word in place of the top scored word. There's no need to change anything in in the suggest() method, so let's place it at the top of top_words().
When to call it? First, if the number of words left to guess is more than 1. Second, if our guesses have met and passed 3. (We will attempt this on guess 3 through 5). Thirdly, if our safetynet attribute is active. (default 0 will evaluate False, but setting a number will use it)
def top_words(self,word_dict,method,n=10):
if (len(self.guess_words) >= 2) and (self.guess_count >= 3) and self.safetynet: #added
print("going into safety mode")
top_unique_words = self.find_unique(rate_of_occurence = self.safetynet)
if top_unique_words:
return top_unique_words[:n]
sorted_words = sorted(word_dict, key=lambda x: (word_dict[x][method]),reverse=True)
top_n = sorted_words[:n]
return top_n
Let's try out 'set_score' on all the missing words above with a safetynet of 2:
Failed words: ['state', 'taunt']
Pretty good. Now we run the full true_fives on rounds of 'set_score' with safetynet set from 1 to 4:
| Word set | Method | Safetynet | Failed Words |
|---|---|---|---|
| true_fives | 'set_score' | 1 | ['booby', 'forge', 'erode', 'gorge', 'grove', 'river', 'drove', 'stake', 'wager', 'skate', 'dirge', 'drier', 'elbow', 'drake', 'eager', 'rarer', 'binge', 'reedy', 'state', 'tight', 'fifth', 'rider', 'rower'] |
| true_fives | 'set_score' | 2 | ['gorge', 'freak', 'woody', 'stake', 'skate', 'drier', 'gazer', 'eager', 'dodgy', 'rarer', 'state'] |
| true_fives | 'set_score' | 3 | ['break', 'brake', 'gorge', 'bread', 'steak', 'stake', 'beard', 'skate', 'dread', 'drier', 'dodgy', 'state', 'goofy'] |
| true_fives | 'set_score' | 4 | ['brake', 'bread', 'steak', 'stake', 'beard', 'skate', 'dread', 'state'] |
Well, we have both regress and progress. When testing on our full true_fives, we don't keep our two failed words from above. On the other hand, our safetynet of 4 has now reduced our missed words from 14 down to 8.
Let's do one more analysis on why this is using the safetynet of 4. When we print out the available words left after each failed word, we have:
| Failed Word | Final guess pool |
|---|---|
| break | ['break', 'brake'] |
| bread | ['bread', 'beard', 'dread'] |
| beard | ['bread', 'beard', 'dread'] |
| dread | ['bread', 'beard', 'dread'] |
| steak | ['steak', 'stake', 'skate', 'state'] |
| stake | ['steak', 'stake', 'skate', 'state'] |
| skate | ['steak', 'stake', 'skate', 'state'] |
| state | ['steak', 'stake', 'skate', 'state'] |
We see a pattern now. The reason our safetynet is not working is because it is looking for unique letters in the whole word, but all these words share the same (or most) letters in their pool. So our last attempt is to adapt our find_unique function to look for unique letters per position.
Let's back up to when the safetynet kicks in and see what its guess pool is:
Word: state After guess 3: ['tease', 'stead', 'stage', 'sweat', 'steak', 'stake', 'skate', 'feast', 'beast', 'stave', 'state']
Transform the words into their postions:
['t', 's', 's', 's', 's', 's', 's', 'f', 'b', 's', 's'],
['e', 't', 't', 'w', 't', 't', 'k', 'e', 'e', 't', 't'],
['a', 'e', 'a', 'e', 'e', 'a', 'a', 'a', 'a', 'a', 'a'],
['s', 'a', 'g', 'a', 'a', 'k', 't', 's', 's', 'v', 't'],
['e', 'd', 'e', 't', 'k', 'e', 'e', 't', 't', 'e', 'e']
So, guessing a word like 'steak' will compress this list down to:
[ 's', 's', 's', 's'],
[ 't', 't', 't', 't'],
[ 'a', 'a', 'a', 'a'],
[ 'g', 'k', 'v', 't'],
[ 'e', 'e', 'e', 'e']
Now the fourth postion as four unique letters. A word like 'gavot' will isolate us down to only one option.
So how can we train our algorithm to do this?
Let's consider a new word list to test. Let's say these are the words in a guess_words pool and we want to find what word will condense it the most.
['watch', 'stage', 'boxer', 'wager', 'gazer', 'stave', 'greed', 'roger']
If we were to guess the word "graph" it would condense the list down to max of two. Let's walk through a tree diagram of this process.
Word: Graph
test 'g':
if True: ['stage','wager','gazer','greed','roger']
test 'r':
if True: ['wager','gazer','greed','roger']
test 'a':
if True: ['wager','gazer']
test 'p'
test 'h'
else: ['greed','roger']
test 'p'
test 'h'
else: ['stage']
else: ['watch','boxer','stave']
test 'r'
if True: ['boxer']
else: ['watch','stave']
test 'a'
test 'p'
test 'h'
if True: ['watch']
else: ['stave']
So what we are looking for is a word that has the fewest maximum leaves at the end of the branches. I found the perfect word to describe this: demarcate.
If we represent the True and False passing as a 1 and 0, respectively, we can build an identifier, or demarcator for each word in the pool as it is matched against the test word. For example, the word 'stage' can be represented as 10100 if tested by 'graph'. So, for all of them:
| word | test | demarcator |
|---|---|---|
| watch | graph | 00101 |
| stage | graph | 10100 |
| boxer | graph | 01000 |
| wager | graph | 11100 |
| gazer | graph | 11100 |
| stave | graph | 00100 |
| greed | graph | 11000 |
| roger | graph | 11000 |
When words share a demarcator, it means they followed the same path of True and False for each letter of the tester. If we count distinct number of demarcators (the number of leaves at the end of the tree above), we will see:
| demarcator | count | words |
|---|---|---|
| 00101 | 1 | ['watch'] |
| 10100 | 1 | ['stage'] |
| 01000 | 1 | ['boxer'] |
| 11100 | 2 | ['wager','gazer'] |
| 00100 | 1 | ['stave'] |
| 11000 | 2 | ['greed','roger'] |
So our tester "graph" can be assigned the metrics:
| word | max-reduced | min-reduced | average-reduced |
|---|---|---|---|
| graph | 2 | 1 | 1.333 |
If we want to find a better word than "Graph" we have to find a word that has either: - fewer max-reduced (all reductions are less than 2, that is: 1, a perfect demarcator) - or if max-reduced is equal, then a smaller min-reduced (not possible in this case) - or if max-reduced and min-reduced are equal, then a smaller average-reduction.
It just so happens a word does exist in the all_source_words dictionary. That word is 'gawds'.
Word: gawds
test 'g':
if True: ['stage','wager','gazer','greed','roger']
test 'a':
if True: ['stage','wager','gazer']
test 'w':
if True: ['wager']
else: ['stage','gazer']
test 'd'
test 's'
if True: ['stage']
else: ['gazer']
else: ['greed','roger']
test 'w'
test 'd'
if True: ['greed']
else: ['roger']
else: ['watch','boxer','stave']
test 'a'
if True: ['watch','stave']
test 'w':
if True: ['watch']
else: ['stave']
else: ['boxer']
| word | test | demarcator |
|---|---|---|
| watch | gawds | 01100 |
| stage | gawds | 11001 |
| boxer | gawds | 00000 |
| wager | gawds | 11100 |
| gazer | gawds | 11000 |
| stave | gawds | 01001 |
| greed | gawds | 10010 |
| roger | gawds | 10000 |
| demarcator | count | words |
|---|---|---|
| 01100 | 1 | ['watch'] |
| 11001 | 1 | ['stage'] |
| 00000 | 1 | ['boxer'] |
| 11100 | 1 | ['wager'] |
| 11000 | 1 | ['gazer'] |
| 01001 | 1 | ['stave'] |
| 10010 | 1 | ['greed'] |
| 10000 | 1 | ['roger'] |
So our tester "gawds" can be assigned the metrics:
| word | max-reduced | min-reduced | average-reduced |
|---|---|---|---|
| graph | 2 | 1 | 1.333 |
| gawds | 1 | 1 | 1 |
"gawds" is a perfect demarcator! Guessing it will return only one valid word left in the pool.
Let's write some code to do this for us.
words_to_reduce = ['watch', 'stage', 'boxer', 'wager', 'gazer', 'stave', 'greed', 'roger']
tester = ['graph','gawds']
ids = dict()
for test in tester:
ids[test] = dict()
for word in words_to_reduce:
word_id = list()
for letter in test:
if letter in word:
word_id.append(1)
else:
word_id.append(0)
ids[test][word] = word_id
The above ids prints:
{'graph': {
'watch': [0, 0, 1, 0, 1],
'stage': [1, 0, 1, 0, 0],
'boxer': [0, 1, 0, 0, 0],
'wager': [1, 1, 1, 0, 0],
'gazer': [1, 1, 1, 0, 0],
'stave': [0, 0, 1, 0, 0],
'greed': [1, 1, 0, 0, 0],
'roger': [1, 1, 0, 0, 0]},
'gawds': {
'watch': [0, 1, 1, 0, 0],
'stage': [1, 1, 0, 0, 1],
'boxer': [0, 0, 0, 0, 0],
'wager': [1, 1, 1, 0, 0],
'gazer': [1, 1, 0, 0, 0],
'stave': [0, 1, 0, 0, 1],
'greed': [1, 0, 0, 1, 0],
'roger': [1, 0, 0, 0, 0]}}
Now we need to count the number of maximum shared ids, minimum shared ids and the average. We will use python's Counter() from the collections library as well as the statistics library.
from collections import Counter
import statistics
#lets drop the name of the words_to_reduce, and simply add the demarcation id as a tuple to the testers.
words_to_reduce = ['watch', 'stage', 'boxer', 'wager', 'gazer', 'stave', 'greed', 'roger']
tester = ['graph','gawds']
ids = dict()
for test in tester:
ids[test] = list()
for word in words_to_reduce:
word_id = list()
for letter in test:
if letter in word:
word_id.append(1)
else:
word_id.append(0)
ids[test][word].append(tuple(word_id))
#The demarcation id needs to be a tuple for the Counter to use it as a dict key.
counts = Counter(ids[test]).values()
id_max = max(counts)
id_min = min(counts)
id_av = statistics.mean(counts)
Now that we have the numbers, we need to add the top performer to a winners list.
...
import math
best_reducer = {
"word":'',
"max": math.inf
"min": math.inf
"mean": math.inf
}
...
for test in tester:
...
if id_max < best_reducer['max']
or id_max == best_reducer['max'] and id_mean < best_reducer['mean']
or id_max == best_reducer['max'] and id_mean == best_reducer['mean'] and id_min < best_reducer['min']:
best_reducer['word'] = test
best_reducer['max'] = id_max
best_reducer['min'] = id_min
best_reducer['mean'] = id_mean
#if we have a perfect demarcator, then no need to look any further
if id_max == 1:
break
So, let's condense all this and put it in a function. And, instead of looping through just two testers, lets loop through all_source_words to find the single best reducer.
def demarcate(words_to_reduce):
best_reducer = {"word":"","max":math.inf,"min":math.inf,"mean":math.inf}
for word in all_source_words:
tester = word
idf = [tuple([1 if l in check else 0 for l in tester ]) for check in words_to_reduce]
counted = Counter(idf).values()
sc_mean = statistics.mean(counted)
sc_max = max(counted)
sc_min = min(counted)
#make some booleans for determining best reducer
smaller_max = sc_max < best_reducer["max"]
eq_max = sc_max == best_reducer["max"]
smaller_mean = sc_mean < best_reducer["mean"]
eq_mean = sc_mean == best_reducer["mean"]
smaller_min = sc_min < best_reducer["min"]
eq_min = sc_min == best_reducer["min"]
if smaller_max or (eq_max and smaller_mean) or (eq_max and eq_mean and smaller_min):
best_reducer = {"word":word,"max":sc_max,"min":sc_min,"mean":sc_mean}
if sc_max == 1:
break
return best_reducer
Played on these sample words_to_reduce we get:
s1 = ['hatch', 'batch', 'patch', 'gatch']
s2 = ['zbcde', 'ybcde', 'xbcde', 'wacde', 'vacde', 'uacde']
s3 = ['watch', 'stage', 'boxer', 'wager', 'gazer', 'stave', 'greed', 'roger']
s4 = ['rover', 'joker', 'skate', 'eager', 'clack', 'greed', 'state', 'roger']
| sample | best reducer | max | min | mean |
|---|---|---|---|---|
| s1 | abamp | 2 | 1 | 1.33 |
| s2 | avyze | 2 | 1 | 1.2 |
| s3 | gawds | 1 | 1 | 1 |
| s4 | kagos | 1 | 1 | 1 |
So even on sample 2 which has a bogus pool, our demarcator can find a good real word solution.
But there's still a problem with our logic. We are only measuring letters in the entire word, this will inevitably run into problems if all the letters in the guessing pool share the same letter. Let's run the function on the word list ['dowry','rowdy','wordy']. The return is:
| sample | best reducer | max | min | mean |
|---|---|---|---|---|
| s5 | aahed | 3 | 3 | 3 |
All three words return the same demarcation id. So we do need to identify letters per slot in addition to their global presence. Testing per slot is, by itself, also insufficient because different words could be missing the same slot letters. So let's use the classic wordle approach of making our id's match a 2,1, or 0 depending on if the letter is in the right position, in the word, or missing. This method is essentially pre-playing the guess for us to find the guess that minimizes the leftovers the most.
def demarcate(self):
best_reducer = {"word":"","max-leftover":math.inf,"min-leftover":math.inf,"mean-leftover":math.inf}
words_to_reduce = self.true_words
for word in self.full_words:
tester = word
idf = [tuple([0 if tester[i] not in check else 2 if tester[i] == check[i] else 1 for i in range(5)]) for check in words_to_reduce]
counted = Counter(idf).values()
sc_mean = statistics.mean(counted)
sc_max = max(counted)
sc_min = min(counted)
smaller_max = sc_max < best_reducer["max-leftover"]
eq_max = sc_max == best_reducer["max-leftover"]
smaller_mean = sc_mean < best_reducer["mean-leftover"]
eq_mean = sc_mean == best_reducer["mean-leftover"]
smaller_min = sc_min < best_reducer["min-leftover"]
eq_min = sc_min == best_reducer["min-leftover"]
if smaller_max or (eq_max and smaller_mean) or (eq_max and eq_mean and smaller_min):
best_reducer = {"word":word,"max-leftover":sc_max,"min-leftover":sc_min,"mean-leftover":sc_mean, "id":idf}
if sc_max == 1:
break
return best_reducer
But wait, at this rate, why are we even using this demarcation function only as a safetynet? Is there any reason why it can't represent the best reducer for every round? Let's give it a try.
If we run our Demarcator on all true_fives, simulating the best first word to guess, it returns:
| sample | best reducer | max | min | mean |
|---|---|---|---|---|
| true_fives | aesir | 183 | 1 | 72.34 |
This is a fantastic start. So let's keep going.
We will bypass self.analyze() , self.count_letters(), self.letter_share(), self.score_words(), self.score_by_letter() and even self.top_words(). We will also not need the self.find_unique().
Instead of these we will go directly from suggest to self.demarcate(), and handle the guessing and evaluation the same.
The downside is it's not very optimized. It takes a long time to cycle through all my true_fives to ensure my win rate. So, since I like to tweak things, I want to find a way to speed this up.
With these optimizations, we can run the demarcator on the true_fives again and find a better starting word
| sample | best reducer | max | min | mean |
|---|---|---|---|---|
| true_fives | aesir | 183 | 1 | 72.34 |
| true_fives | raise | 167 | 1 | 17.49 |
Knowing the first guess, we can slip a bypass at the beginning of the demarcator to check if this is the first guess. No need to run the sorting on the biggest set of words when it will always return the same word.
def demarcate(self):
...
if self.guess_count == 0:
return {'word': 'raise','max-leftover': 167,'min-leftover': 1,'mean-leftover': 17.49}
...
...
Let's clean things up and label our functions
from nytimesWordlejs import true_fives
from collections import Counter
import statistics
import math
class wordle():
def __init__(self, possible_words: list=true_fives):
"""Instantiate the game with a list of words to play from. Default Wordle potential answers"""
self.words_to_reduce = possible_words
self.true_fives = possible_words.copy()
self.game_word = ""
self.suggestions = []
self.guesses=[]
self.guess_count = 0
def set_word(self, word_to_use : str) -> None:
"""For self playing or testing, give the game a word to use."""
self.game_word = word_to_use
def suggest(self) -> dict:
"""Returns a dictionary with minimum key 'word' to suggest as the next word to guess """
if len(self.words_to_reduce) <= 2:
return {'word':self.words_to_reduce[0]}
self.suggestions.append(self.demarcate())
return self.suggestions[-1]
def guess(self, word: str, manual:bool =False) -> dict:
"""Generates a guess evaluation and returns a dict with boolean key 'won' to mark status of game"""
word = word.lower()
response = {'won':False,'code':[],'word':word}
# the manual parameter allows us to manually play by inserting our own code
if not manual:
for i,l in enumerate(word):
if l==self.game_word[i]:
response['code'].append(2)
elif l in self.game_word:
response['code'].append(1)
else:
response['code'].append(0)
else:
response['code'] = manual
self.guesses.append(word)
self.guess_count += 1
if word == self.game_word:
response['won'] = True
return response
self.evaluate(response)
return response
def evaluate(self, guess_response: dict) -> None:
"""Rebuilds words in self.words_to_reduce based on word and code keys in parameter"""
code = guess_response['code']
guess = guess_response['word']
for i,c, in enumerate(code):
letter = guess[i]
if c == 2:
#if the letter is in the right position, keep all those words who have this letter in this position
self.words_to_reduce = [word for word in self.words_to_reduce if word[i]==letter]
elif c == 1:
#if the letter is in the word, keep all words who have this letter but NOT in this position
self.words_to_reduce = [word for word in self.words_to_reduce if (letter in word) and (word[i] is not letter)]
else:
#keep remaining words if they do not have this letter
self.words_to_reduce = [word for word in self.words_to_reduce if (letter not in word)]
def demarcate(self) -> dict:
"""
Generates unique identifiers for every combination of self.true_fives and self.words_to_reduce.
Returns the word with stats (as a dict) which produces the fewest duplicate identifiers
"""
best_reducer = {"word":"","max":math.inf,"min":math.inf,"mean":math.inf}
if self.guess_count == 0:
return {'word': 'raise','max': 167,'min': 1,'mean': 17.49}
#T is the Transformed list, with each row holding all letters in the index position
T = [l for l in zip(*self.words_to_reduce)]
for word in self.true_fives:
score = 0
for letter, position in zip(word, T):
#If all letters in position are unique
if len(set(position)) > 1:
#If the letter of potential guess word is one of the unique letters in this postion
if letter in position:
score+=1
else:
#all letters in position are the same, give this slot a freebee
score+=1
if score < 5:
#Essentially, every letter must have a valuable contribution in order to pass
#Words whose letters do not all contribute are now skipped
continue
#list comprehension to generate an id for each word
idf = [tuple([0 if word[i] not in check else 2 if word[i] == check[i] else 1 for i in range(5)]) for check in self.words_to_reduce]
#count how many times word id's occur. The fewer the id count, the better the word is at reducing the guessing pool
counted = Counter(idf).values()
sc_mean = statistics.mean(counted)
sc_max = max(counted)
sc_min = min(counted)
#prepare to compare this word score with the current best
smaller_max = sc_max < best_reducer["max"]
eq_max = sc_max == best_reducer["max"]
smaller_mean = sc_mean < best_reducer["mean"]
eq_mean = sc_mean == best_reducer["mean"]
smaller_min = sc_min < best_reducer["min"]
eq_min = sc_min == best_reducer["min"]
#sort through the score to determine if it is better than the current best
if smaller_max or (eq_max and smaller_mean) or (eq_max and eq_mean and smaller_min):
best_reducer = {"word":word,"max":sc_max,"min":sc_min,"mean":sc_mean, "id":idf}
#if the word generates 100% unique ids, then it is a perfect demarcator, and we don't need to search any further
if sc_max == 1:
break
return best_reducer
def self_test(self, word_to_play: str) -> dict:
"""Simulate a round of play, assiging a word from parameter and returning boolean win and number of guesses in a dict"""
self.set_word(word_to_play)
won = False
while True:
s = self.suggest()
g = self.guess(s['word'])
if g['word'] == self.game_word:
won = True
break
if self.guess_count >= 6:
break
self.evaluate(g)
performance = {
"won":won,
"attempts":self.guess_count
}
return performance
def test_performance():
cycle = 0
losses = 0
lost_words = []
total_guesses = 0
guess_tally = []
for test_word in true_fives:
cycle += 1
clear_output(wait=True)
display(cycle)
game = wordle_game_2p0()
results = game.self_test(test_word)
total_guesses += game.guess_count
guess_tally.append(game.guess_count)
if not results['won']:
losses += 1
lost_words.append(test_word)
ct = Counter(guess_tally)
performance = {"Win ratio": 100 - losses/cycle * 100, "average guesses": total_guesses/cycle, "counter guesses":ct}
return performance
Method < demarcate > wins 100.0% with average 3.5969 attempts
And for some more insight:
| Number of Guesses | Number of words |
|---|---|
| 1 | 1 |
| 2 | 64 |
| 3 | 940 |
| 4 | 1179 |
| 5 | 124 |
| 6 | 7 |
I have two versions of play at this time. I have a .py file which you can run in terminal Github. I also have a flask webapp running HERE
Thank you for making it to the end. Possitive vibes appreciated, and keep on coding!